
【題目】新高考![]() 最大的特點就是取消文理分科,除語文、數學、外語之外,從物理、化學、生物、政治、歷史、地理這6科中自由選擇三門科目作為選考科目.某研究機構為了了解學生對全文(選擇政治、歷史、地理)的選擇是否與性別有關,從某學校高一年級的1000名學生中隨機抽取男生,女生各25人進行模擬選科.經統計,選擇全文的人數比不選全文的人數少10人.
最大的特點就是取消文理分科,除語文、數學、外語之外,從物理、化學、生物、政治、歷史、地理這6科中自由選擇三門科目作為選考科目.某研究機構為了了解學生對全文(選擇政治、歷史、地理)的選擇是否與性別有關,從某學校高一年級的1000名學生中隨機抽取男生,女生各25人進行模擬選科.經統計,選擇全文的人數比不選全文的人數少10人.
(1)估計在男生中,選擇全文的概率.
(2)請完成下面的![]() 列聯表;并估計有多大把握認為選擇全文與性別有關,并說明理由;
列聯表;并估計有多大把握認為選擇全文與性別有關,并說明理由;
選擇全文 | 不選擇全文 | 合計 | |
男生 | 5 | ||
女生 | |||
合計 |
附: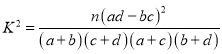 ,其中
,其中![]() .
.
P( | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.076 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]() .
.
(1)若曲線![]() 在
在![]() 處的切線的方程為
處的切線的方程為![]() ,求實數
,求實數![]() 的值;
的值;
(2)設![]() ,若對任意兩個不等的正數
,若對任意兩個不等的正數![]() ,都有
,都有![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍;
的取值范圍;
(3)若在![]() 上存在一點
上存在一點![]() ,使得
,使得![]() 成立,求實數
成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分14分)
已知![]() ,
, ![]() 為橢圓
為橢圓![]() 的左、右頂點,
的左、右頂點, ![]() 為其右焦點,
為其右焦點, ![]() 是橢圓
是橢圓![]() 上異于
上異于![]() ,
, ![]() 的動點,且
的動點,且![]() 面積的最大值為
面積的最大值為![]() .
.
(Ⅰ)求橢圓![]() 的方程及離心率;
的方程及離心率;
(Ⅱ)直線![]() 與橢圓在點
與橢圓在點![]() 處的切線交于點
處的切線交于點![]() ,當直線
,當直線![]() 繞點
繞點![]() 轉動時,試判斷以
轉動時,試判斷以![]()
為直徑的圓與直線![]() 的位置關系,并加以證明.
的位置關系,并加以證明.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數![]() ,函數
,函數![]() ,
,![]() ,其中
,其中![]() 為常數,且
為常數,且![]() ,令函數
,令函數![]() 為函數
為函數![]() 和
和![]() 的積函數.
的積函數.
(1)求函數![]() 的表達式,并求其定義域;
的表達式,并求其定義域;
(2)當![]() 時,求函數
時,求函數![]() 的值域
的值域
(3)是否存在自然數![]() ,使得函數
,使得函數![]() 的值域恰好為
的值域恰好為![]() ?若存在,試寫出所有滿足條件的自然數
?若存在,試寫出所有滿足條件的自然數![]() 所構成的集合;若不存在,試說明理由.
所構成的集合;若不存在,試說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨機抽取某中學甲、乙兩班各10名同學,測量他們的身高(單位:cm),獲得身高數據的莖葉圖如圖7.

(1)根據莖葉圖判斷哪個班的平均身高較高;
(2)計算甲班的樣本方差;
(3)現從乙班這10名同學中隨機抽取兩名身高不低于173cm的同學,求身高為176cm的同學被抽中的概率。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知橢圓![]() (a>b>0)的離心率
(a>b>0)的離心率![]() ,過點A(0,-b)和B(a,0)的直線與原點的距離為
,過點A(0,-b)和B(a,0)的直線與原點的距離為![]() .
.

(1)求橢圓的方程.
(2)已知定點E(-1,0),若直線y=kx+2(k≠0)與橢圓交于C、D兩點.問:是否存在k的值,使以CD為直徑的圓過E點?請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖1,在高為2的梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,過
,過![]() 、
、![]() 分別作
分別作![]() ,
,![]() ,垂足分別為
,垂足分別為![]() 、
、![]() .已知
.已知![]() ,將梯形
,將梯形![]() 沿
沿![]() 、
、![]()
同側折起,使得![]() ,
,![]() ,得空間幾何體
,得空間幾何體![]() ,如圖2.
,如圖2.


(Ⅰ)證明:![]() ;
;
(Ⅱ)求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】![]() 賽季的歐洲冠軍聯賽八分之一決賽的首回合較量將于北京時間2018年2月15日3:45在伯納烏球場打響.由
賽季的歐洲冠軍聯賽八分之一決賽的首回合較量將于北京時間2018年2月15日3:45在伯納烏球場打響.由![]() 羅領銜的衛冕冠軍皇家馬德里隊(以下簡稱“皇馬”)將主場迎戰剛剛創下歐冠小組賽最多進球記錄的法甲領頭羊巴黎圣日曼隊(以下簡稱“巴黎”),激烈對決,一觸即發.比賽分上,下兩個半場進行,現在有加泰羅尼亞每題測皇馬,巴黎的每半場進球數及概率如表:
羅領銜的衛冕冠軍皇家馬德里隊(以下簡稱“皇馬”)將主場迎戰剛剛創下歐冠小組賽最多進球記錄的法甲領頭羊巴黎圣日曼隊(以下簡稱“巴黎”),激烈對決,一觸即發.比賽分上,下兩個半場進行,現在有加泰羅尼亞每題測皇馬,巴黎的每半場進球數及概率如表:
0 | 1 | 2 | |
巴黎 |
|
|
|
皇馬 |
|
|
|
(1)按照預測,求巴黎在比賽中至少進兩球的概率;
(2)按照預測,若設![]() 為皇馬總進球數,
為皇馬總進球數,![]() 為巴黎總進球數,求
為巴黎總進球數,求![]() 和
和![]() 的分布列,并判斷
的分布列,并判斷![]() 和
和![]() 的大小.
的大小.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com