已知{
an}為等差數(shù)列,
a1+
a3+
a5=105,
a2+
a4+
a6=99,以
Sn表示數(shù)列{
an}的前
n項(xiàng)和,則使得
Sn達(dá)到最大值的
n是( )
解:設(shè){an}的公差為d,由題意得
a1+a3+a5=a1+a1+2d+a1+4d=105,即a1+2d=35,①
a2+a4+a6=a1+d+a1+3d+a1+5d=99,即a1+3d=33,②
由①②聯(lián)立得a1=39,d=-2,
∴sn="39n+n(n-1)" 2 ×(-2)=-n2+40n=-(n-20)2+400,
故當(dāng)n=20時(shí),Sn達(dá)到最大值400.
故選B.
練習(xí)冊系列答案
相關(guān)習(xí)題
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
若兩等差數(shù)列
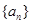
、
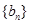
前
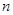
項(xiàng)和分別為
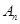
、
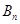
,滿足
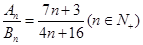
,
則
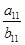
的值為( )
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
.(本小題滿分12分) 已知等差數(shù)列
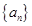
滿足:

,
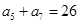
,
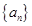
的前
n項(xiàng)和為
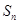
.
(Ⅰ)求通項(xiàng)公式
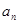
及前
n項(xiàng)和
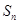
;
(Ⅱ)令
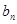
=
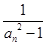
(
n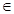
N
*),求數(shù)列
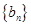
的前
n項(xiàng)和
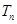
.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
設(shè)
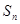
是等差數(shù)列
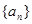
的前n項(xiàng)和,已知
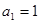
,公差d=2,則
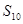
="_______" .
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
等差數(shù)列
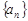
的前
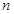
項(xiàng)和為
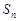
,
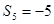
,
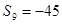
,則
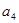
的值為( )
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
在數(shù)列
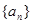
中,若
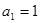
,
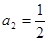
,
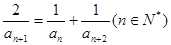
,則該數(shù)列的通項(xiàng)為
.

查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
設(shè)
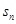
是等差數(shù)列{
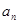
}的前n項(xiàng)和,已知
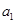
=3,
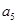
=11,則
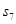
等于_________
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
在等差數(shù)列
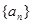
中,
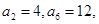
則公差d= ( )
查看答案和解析>>


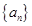 滿足:
滿足: ,
,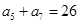 ,
,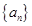 的前n項(xiàng)和為
的前n項(xiàng)和為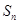 .
.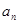 及前n項(xiàng)和
及前n項(xiàng)和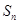 ;
; 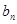 =
=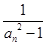 (n
(n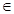 N*),求數(shù)列
N*),求數(shù)列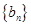 的前n項(xiàng)和
的前n項(xiàng)和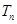 .
.