
 ,所表示的平面區域是以A(
,所表示的平面區域是以A( )、B(
)、B( )、O(0,0)為頂點的△AOB的邊界及其內部,作直線l:y=-x.由圖形可知,把直線l平移至過點B(
)、O(0,0)為頂點的△AOB的邊界及其內部,作直線l:y=-x.由圖形可知,把直線l平移至過點B( )時,z取最大值.
)時,z取最大值. 解:設桌子、椅子各買x張和y張,則所買桌椅的總數為z=x+y.
解:設桌子、椅子各買x張和y張,則所買桌椅的總數為z=x+y. 其中x,y∈N+.…(4分)
其中x,y∈N+.…(4分)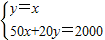 解得
解得
 解得
解得 …(6分)
…(6分) ),點B的坐標為(
),點B的坐標為( ),
),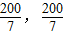 )、
)、 )、O(0,0)為頂點的△AOB的邊界及其內部(如圖中陰影所示). …(9分)
)、O(0,0)為頂點的△AOB的邊界及其內部(如圖中陰影所示). …(9分) )時,亦即x=25,
)時,亦即x=25, 時,z取最大值.
時,z取最大值.

 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源:2005年廣東省廣州市高二數學水平測試試卷(解析版) 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com