
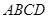 的邊長為
的邊長為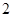 ,
,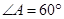 ,
,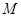 為
為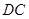 的中點,則
的中點,則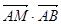 的值為 .
的值為 .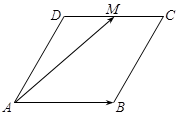
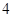
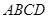 的邊長為
的邊長為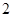 ,
,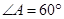 ,
,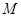 為
為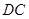 的中點,先以點A位坐標(biāo)原點建立的直角坐標(biāo)系,求出其它各點的坐標(biāo),然后利用點的坐標(biāo)表示出
的中點,先以點A位坐標(biāo)原點建立的直角坐標(biāo)系,求出其它各點的坐標(biāo),然后利用點的坐標(biāo)表示出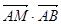
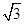 ),D(1,
),D(1,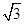 ),M(2,
),M(2,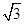 )
)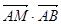 =4,故可知答案為4.
=4,故可知答案為4.

 小學(xué)奪冠AB卷系列答案
小學(xué)奪冠AB卷系列答案湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com