
(本小題滿分12分)
已知數列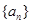 和
和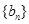 滿足:
滿足: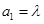 ,
,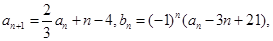 其中
其中 為實數,
為實數,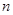 為正整數.
為正整數.
(1)對任意實數 ,證明數列
,證明數列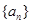 不是等比數列;
不是等比數列;
(2)試判斷數列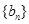 是否為等比數列,并證明你的結論;
是否為等比數列,并證明你的結論;
(3)設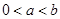 ,
,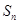 為數列
為數列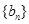 的前
的前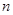 項和.是否存在實數
項和.是否存在實數 ,使得對任意正整數
,使得對任意正整數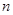 ,都有
,都有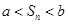 ?若存在,求
?若存在,求 的取值范圍;若不存在,說明理由.
的取值范圍;若不存在,說明理由.
(1)見解析;(2)見解析;(3)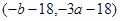 。
。
解析試題分析:(1)證明:假設存在一個實數 ,使{
,使{ }是等比數列, 則有
}是等比數列, 則有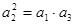 ,即
,即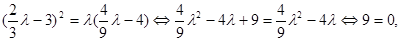 矛盾.
矛盾.
所以{ }不是等比數列.
}不是等比數列.
(2)解:因為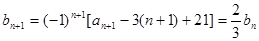
又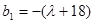 ,所以
,所以
當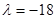 ,
,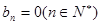 ,此時
,此時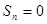
當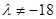 時,
時,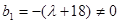 ,
, 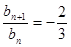
 ,
,
此時,數列{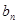 }是以
}是以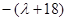 為首項,
為首項,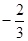 為公比的等比數列.
為公比的等比數列.
∴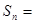

(3)要使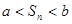 對任意正整數
對任意正整數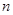 成立,
成立,
即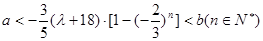
得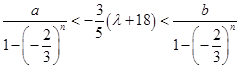 (1)
(1)
令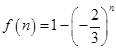 ,則當
,則當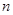 為正奇數時,
為正奇數時,
∴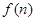 的最大值為
的最大值為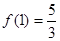 ,
, 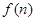 的最小值為
的最小值為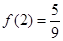 ,
,
于是,由(1)式得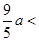
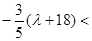

當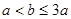 時,由
時,由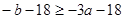 ,不存在實數滿足題目要求
,不存在實數滿足題目要求
當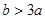 存在實數
存在實數 ,使得對任意正整數
,使得對任意正整數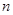 ,都有
,都有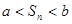 ,且
,且 的取值范圍是
的取值范圍是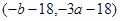 。
。
考點:本題考查等比數列的簡單性質。
點評:本題屬于數列綜合運用題,考查了由所給的遞推關系證明數列的性質,對所給的遞推關系進行研究求數列的遞推公式以及利用數列的求和公式求其和,再由和的存在范圍確定使得不等式成立的參數的取值范圍,難度較大,綜合性很強,對答題者探究的意識與探究規律的能力要求較高,是一道能力型題.


 浙大優學小學年級銜接捷徑浙江大學出版社系列答案
浙大優學小學年級銜接捷徑浙江大學出版社系列答案科目:高中數學 來源: 題型:解答題
(本小題滿分12分)
已知數列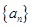 的前
的前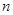 項和為
項和為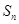 滿足:
滿足: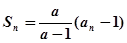 (
(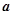 為常數,且
為常數,且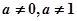 )
)
(1)若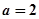 ,求數列
,求數列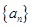 的通項公式
的通項公式
(2)設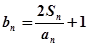 ,若數列
,若數列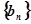 為等比數列,求
為等比數列,求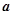 的值.
的值.
(3)在滿足條件(2)的情形下,設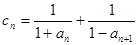 ,數列
,數列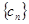 前
前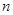 項和為
項和為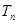 ,求證
,求證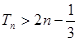
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分13分)
已知數列{an}的首項a1=" t" >0, ,n=1,2,……
,n=1,2,……
(1)若t = ,求
,求 是等比數列,并求出{an}的通項公式;
是等比數列,并求出{an}的通項公式;
(2)若 對一切
對一切 都成立,求t的取值范圍.
都成立,求t的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
設數列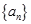 的前n項和為
的前n項和為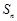 ,且滿足
,且滿足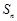 =2-
=2-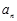 ,
,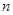 =1,2,3,….
=1,2,3,….
(1)求數列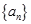 的通項公式;
的通項公式;
(2)若數列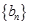 滿足
滿足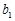 =1,且
=1,且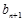 =
=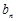 +
+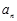 ,求數列
,求數列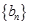 的通項公式;
的通項公式;
(3)設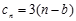 ,求數列
,求數列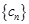 的前
的前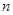 項和為
項和為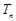 .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com