
【題目】如圖,正三棱柱![]() 的所有棱長均
的所有棱長均![]() ,
,![]() 為棱
為棱![]() (不包括端點)上一動點,
(不包括端點)上一動點,![]() 是
是![]() 的中點.
的中點.
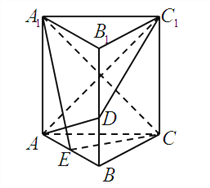
(Ⅰ)若![]() ,求
,求![]() 的長;
的長;
(Ⅱ)當![]() 在棱
在棱![]() (不包括端點)上運動時,求平面
(不包括端點)上運動時,求平面![]() 與平面
與平面![]() 的夾角的余弦值的取值范圍.
的夾角的余弦值的取值范圍.
【答案】(Ⅰ)BD=1;(Ⅱ)(![]() ,
,![]() ].
].
【解析】【試題分析】(I)由![]() 得到
得到![]() 平面
平面![]() ,所以
,所以![]() ,由于
,由于![]() ,所以
,所以![]() 平面
平面![]() ,所以
,所以![]() ,由此得到
,由此得到![]() 為
為![]() 的中點,所以
的中點,所以![]() .(I)以
.(I)以![]() 為空間坐標原點建立空間直角坐標系,利用兩個平面的法向量來求得它們夾角的余弦值的取值范圍.
為空間坐標原點建立空間直角坐標系,利用兩個平面的法向量來求得它們夾角的余弦值的取值范圍.
【試題解析】
證明:(Ⅰ),由AC=BC,AE=BE,知CE⊥AB,
又平面ABC⊥平面ABB1A1,所以CE⊥平面ABB1A1
而AD平面ABB1A1,∴AD⊥CE,又AD⊥A1C所以AD⊥平面A1CE,
所以AD⊥A1E.易知此時D為BB1的中點,故BD=1.
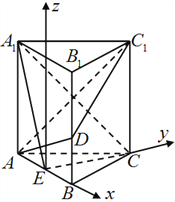
(Ⅱ)以E為原點,EB為x軸,EC為y軸,
過E作垂直于平面ABC的垂線為z軸,
建立空間直角坐標系,設BD=t,
則A(-1,0,0),D(1,0,t),C1(0,![]() ,2),
,2),
![]() =(2,0,t),
=(2,0,t),![]() =(1,
=(1,![]() ,2),設平面ADC1的法向量
,2),設平面ADC1的法向量![]() =(x,y,z),
=(x,y,z),
則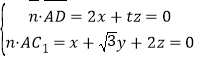 ,取x=1,得
,取x=1,得![]() ,
,
平面ABC的法向量![]() =(0,01),設平面ADC1與平面ABC的夾角為θ,
=(0,01),設平面ADC1與平面ABC的夾角為θ,
∴cosθ=![]() =
=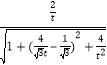 =
=![]() =
=![]()
由于t∈(0,2),故cosθ∈(![]() ,
,![]() ].
].
即平面ADC1與平面ABC的夾角的余弦值的取值范圍為(![]() ,
,![]() ].
].


科目:高中數學 來源: 題型:
【題目】在直角坐標系中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數,
為參數,![]() ),在以坐標原點為極點,
),在以坐標原點為極點,![]() 軸非負軸為極軸的極坐標系中,曲線
軸非負軸為極軸的極坐標系中,曲線![]() :
:![]() (
(![]() 為極角).
為極角).
(1)將曲線![]() 化為極坐標方程,當
化為極坐標方程,當![]() 時,將
時,將![]() 化為直角坐標方程;
化為直角坐標方程;
(2)若曲線![]() 與
與![]() 相交于一點
相交于一點![]() ,求
,求![]() 點的直角坐標使
點的直角坐標使![]() 到定點
到定點![]() 的距離最小.
的距離最小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下表提供了某廠節能降耗技術改造后生產甲產品過程中記錄的產量![]() (噸)與相應的生產能耗
(噸)與相應的生產能耗![]() (噸)標準煤的幾組對照數據:
(噸)標準煤的幾組對照數據:
![]()
(1)請根據上表提供的數據,用最小二乘法求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(2)已知該廠技改前,100噸甲產品的生產能耗為90噸標準煤.試根據(1)求出的線性回歸方程,預測生產100噸甲產品的生產能耗比技改前降低多少噸標準煤?
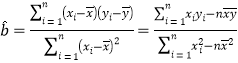 ,參考數值:
,參考數值:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在邊長為4的菱形![]() 中,
中,![]() ,點
,點![]() 分別是邊
分別是邊![]() 的中點,
的中點,![]() ,沿
,沿![]() 將
將![]() 翻折到
翻折到![]() ,連接
,連接![]() ,得到如圖所示的五棱錐,且
,得到如圖所示的五棱錐,且![]() .
.
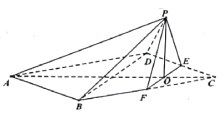
(1)求證:平面![]() 平面
平面![]() ;
;
(2)求平面![]() 與平面
與平面![]() 所成二面角的余弦值.
所成二面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校為了推動數學教學方法的改革,學校將高一年級部分生源情況基本相同的學生分成甲、乙兩個班,每班各40人,甲班按原有模式教學,乙班實施教學方法改革.經過一年的教學實驗,將甲、乙兩個班學生一年來的數學成績取平均數,兩個班學生的平均成績均在![]() ,按照區間
,按照區間![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 進行分組,繪制成如下頻率分布直方圖,規定不低于80分(百分制)為優秀.
進行分組,繪制成如下頻率分布直方圖,規定不低于80分(百分制)為優秀.

完成表格,并判斷是否有![]() 以上的把握認為“數學成績優秀與教學改革有關”;
以上的把握認為“數學成績優秀與教學改革有關”;

(2)從乙班![]() ,
,![]() ,
,![]() 分數段中,按分層抽樣隨機抽取7名學生座談,從中選三位同學發言,記來自
分數段中,按分層抽樣隨機抽取7名學生座談,從中選三位同學發言,記來自![]() 發言的人數為隨機變量
發言的人數為隨機變量![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【2018安徽江南十校高三3月聯考】線段![]() 為圓
為圓![]() :
: ![]() 的一條直徑,其端點
的一條直徑,其端點![]() ,
, ![]() 在拋物線
在拋物線![]() :
: ![]() 上,且
上,且![]() ,
, ![]() 兩點到拋物線
兩點到拋物線![]() 焦點的距離之和為
焦點的距離之和為![]() .
.
(I)求直徑![]() 所在的直線方程;
所在的直線方程;
(II)過![]() 點的直線
點的直線![]() 交拋物線
交拋物線![]() 于
于![]() ,
, ![]() 兩點,拋物線
兩點,拋物線![]() 在
在![]() ,
, ![]() 處的切線相交于
處的切線相交于![]() 點,求
點,求![]() 面積的最小值.
面積的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數y=f(x)是定義在R上的偶函數,對于x∈R,都有f(x+4)=f(x)+f(2)成立,當x1,x2∈[0,2]且x1≠x2時,都有![]() 給出下列四個命題:
給出下列四個命題:
①f(﹣2)=0;
②直線x=﹣4是函數y=f(x)的圖象的一條對稱軸;
③函數y=f(x)在[4,6]上為減函數;
④函數y=f(x)在(﹣8,6]上有四個零點.
其中所有正確命題的序號為_____.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com