
【題目】選修4﹣4:坐標系與參數方程
在平面直角坐標系x0y中,動點A的坐標為(2﹣3sinα,3cosα﹣2),其中α∈R.在極坐標系(以原點O為極點,以x軸非負半軸為極軸)中,直線C的方程為ρcos(θ﹣ ![]() )=a.
)=a.
(1)判斷動點A的軌跡的形狀;
(2)若直線C與動點A的軌跡有且僅有一個公共點,求實數a的值.
【答案】
(1)解:設動點A的直角坐標為(x,y),則 ![]() ,利用同角三角函數的基本關系消去參數α可得,
,利用同角三角函數的基本關系消去參數α可得,
(x﹣2)2+(y+2)2=9,點A的軌跡為半徑等于3的圓.
(2)解:把直線C方程為ρcos(θ﹣ ![]() )=a化為直角坐標方程為
)=a化為直角坐標方程為 ![]() +
+ ![]() =2a,
=2a,
由題意可得直線C與圓相切,故有 ![]() =3,解得 a=3 或a=﹣3.
=3,解得 a=3 或a=﹣3.
【解析】(1)設動點A的直角坐標為(x,y),則 ![]() ,利用同角三角函數的基本關系消去參數α可得直角坐標方程,從而得到點A的軌跡.(2)把直線C方程為直角坐標方程,由題意可得直線C與圓相切,故有圓心到直線的距離等于半徑,由此解得 a 的值.
,利用同角三角函數的基本關系消去參數α可得直角坐標方程,從而得到點A的軌跡.(2)把直線C方程為直角坐標方程,由題意可得直線C與圓相切,故有圓心到直線的距離等于半徑,由此解得 a 的值.
【考點精析】解答此題的關鍵在于理解圓的參數方程的相關知識,掌握圓![]() 的參數方程可表示為
的參數方程可表示為![]() .
.


科目:高中數學 來源: 題型:
【題目】已知f(x)=2x,g(x)是一次函數,并且點(2,2)在函數f[(g(x)]的圖象上,點(2,5)在函數g[f(x)]的圖象上,則g(x)的解析式為_____.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系xoy中,曲線C1: ![]() (t為參數,t≠0),其中0≤α<π,在以O為極點,x軸正半軸為極軸的極坐標系中,曲線C2:ρ=2sinθ,曲線C3:ρ=2
(t為參數,t≠0),其中0≤α<π,在以O為極點,x軸正半軸為極軸的極坐標系中,曲線C2:ρ=2sinθ,曲線C3:ρ=2 ![]() cosθ.
cosθ.
(1)求C2與C3交點的直角坐標;
(2)若C2與C1相交于點A,C3與C1相交于點B,求|AB|的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,內角A,B,C的對邊分別是a,b,c,已知c=6,sinA﹣sinC=sin(A﹣B).若1≤a≤6,則sinC的取值范圍是 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某食品的保鮮時間t(單位:小時)與儲藏溫度x(單位:℃)滿足函數關系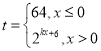 且該食品在4℃的保鮮時間是16小時.
且該食品在4℃的保鮮時間是16小時.
已知甲在某日上午10時購買了該食品,并將其遺放在室外,且此日的室外溫度隨時間變化如圖所示.給出以下四個結論:

①該食品在6℃的保鮮時間是8小時;
②當x∈[﹣6,6]時,該食品的保鮮時間t隨著x增大而逐漸減少;
③到了此日13時,甲所購買的食品還在保鮮時間內;
④到了此日14時,甲所購買的食品已然過了保鮮時間.
其中,所有正確結論的序號是 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數g(x)=ax2-2ax+1+b(a>0)在區間[2,4]上的最大值為9,最小值為1,記f(x)=g(|x|)。
(1)求實數a,b的值;
(2)若不等式f(2k)>1成立,求實數k的取值范圍;
(3)定義在[p,q]上的函數![]() (x),設p=x0<x1<…<xi-1<xi<…<xn=q,x1,x2,…,xn-l將區間[p,q]任意劃分成n個小區間,如果存在一個常數M>0,使得和式
(x),設p=x0<x1<…<xi-1<xi<…<xn=q,x1,x2,…,xn-l將區間[p,q]任意劃分成n個小區間,如果存在一個常數M>0,使得和式![]() 恒成立,則稱函數
恒成立,則稱函數![]() (x)為在[p,q]上的有界變差函數。試判斷函數f(x)是否為在[0,4]上的有界變差函數?若是,求M的最小值;若不是,請說明理由。
(x)為在[p,q]上的有界變差函數。試判斷函數f(x)是否為在[0,4]上的有界變差函數?若是,求M的最小值;若不是,請說明理由。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓 ![]() 的右焦點為F(2,0),M為橢圓的上頂點,O為坐標原點,且△MOF是等腰直角三角形.
的右焦點為F(2,0),M為橢圓的上頂點,O為坐標原點,且△MOF是等腰直角三角形.
(1)求橢圓的方程;
(2)過點M分別作直線MA,MB交橢圓于A,B兩點,設兩直線的斜率分別為k1 , k2 , 且k1+k2=8,證明:直線AB過定點( ![]() ).
).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在如圖所示的幾何體中,四邊形![]() 為矩形,平面
為矩形,平面![]() ,
, ![]() //
// ![]() ,
,![]() ,
, ![]() ,點
,點![]() 點P在棱
點P在棱![]() 上.
上.
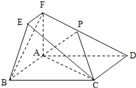
(1)求證: ![]() ;
;
(2)若![]() 是
是![]() 的中點,求異面直線
的中點,求異面直線![]() 與
與![]() 所成角的余弦值;
所成角的余弦值;
(3)是否存在正實數![]() ,使得
,使得![]() ,且滿足二面角
,且滿足二面角![]() 的余弦值為
的余弦值為![]() ,若存在,求出
,若存在,求出![]() 的值,若不存在,請說明理由.
的值,若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com