
設函數f(x)=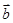 ×
×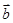 ,其中向量
,其中向量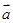 ="(2cosx,1),"
="(2cosx,1)," 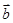 =(cosx,
=(cosx,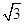 sin2x+m).
sin2x+m).
(1)求函數f(x)的最小正周期和f(x)在[0, p]上的單調遞增區間;
(2)當xÎ[0 ]時,ô f(x)ô <4恒成立,求實數m的取值范圍.
]時,ô f(x)ô <4恒成立,求實數m的取值范圍.
(1) f(x)的最小正周期T=p,在[0, p]上的單調遞增區間為[0, ],[
],[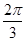 ,p];
,p];
(2) -4<m<1.
解析試題分析:(1)f(x)= 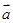 ×
×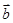 =2cos2x+
=2cos2x+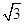 sin2x+m 1分
sin2x+m 1分
=cos2x+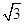 sin2x+m+1=2sin(2x+
sin2x+m+1=2sin(2x+ )+m+1 3分
)+m+1 3分
∴f(x)的最小正周期T=p, 4分
在[0, p]上的單調遞增區間為[0, ],[
],[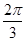 ,p] 6分
,p] 6分
(2)∵當xÎ[0, ]時,
]時,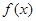 遞增,當xÎ[
遞增,當xÎ[ ,
, ]時,
]時,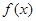 遞減,
遞減,
∴當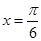 時,
時,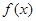 的最大值等于
的最大值等于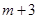 . 8分
. 8分
當x= 時,
時,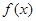 的最小值等于m. 10分
的最小值等于m. 10分
由題設知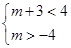 解之得,-4<m<1. 12分
解之得,-4<m<1. 12分
考點:本題主要考查平面向量的數量積,平面向量的坐標運算,三角函數的和差倍半公式,三角函數的圖象和性質。
點評:中檔題,本題綜合考查平面向量的數量積,平面向量的坐標運算,三角函數的和差倍半公式,三角函數、二次函數的圖象和性質。利用向量的運算,得到三角函數式,運用三角公式進行化簡,以便于利用其它知識解題,是這類題的顯著特點。本題(2)涉及角的范圍,易于出錯。


科目:高中數學 來源: 題型:
| π |
| 4 |
| 5π |
| 8 |
| 7π |
| 8 |
| π |
| 8 |
| 3π |
| 8 |
| π |
| 8 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 |
| 2 |
| 2x+t |
| x2-3 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 2x2 | x+1 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com