
【題目】已知圓 ![]() :
: ![]() ,直線
,直線 ![]() :
: ![]() .
.
(1)設點 ![]() 是直線
是直線 ![]() 上的一動點,過
上的一動點,過 ![]() 點作圓
點作圓 ![]() 的兩條切線,切點分別為
的兩條切線,切點分別為 ![]() ,求四邊形
,求四邊形 ![]() 的面積的最小值;
的面積的最小值;
(2)過 ![]() 作直線
作直線 ![]() 的垂線交圓
的垂線交圓 ![]() 于
于 ![]() 點,
點, ![]() 為
為 ![]() 關于
關于 ![]() 軸的對稱點,若
軸的對稱點,若 ![]() 是圓
是圓 ![]() 上異于
上異于 ![]() 的兩個不同點,且滿足:
的兩個不同點,且滿足: ![]() ,試證明直線
,試證明直線 ![]() 的斜率為定值.
的斜率為定值.
【答案】
(1)解:設四邊形 ![]() 的面積為
的面積為 ![]() ,
, ![]() ,
,![]() ,所以,當
,所以,當 ![]() 最小時,
最小時, ![]() 就最小,
就最小,![]() ,所以:
,所以: ![]()
(2)解:直線 ![]() 的方程為:
的方程為: ![]() ,代入
,代入 ![]() ,且
,且 ![]() 在第一象限,得
在第一象限,得 ![]() 則
則 ![]() .設
.設 ![]() ,
, ![]() ,
,![]() ,
, ![]() 設直線
設直線 ![]() 的斜率為
的斜率為 ![]() ,則
,則 ![]() 斜率為
斜率為 ![]() ,
,![]() ,
, ![]() ,
,
聯立 ![]() 消
消 ![]() 得:
得: ![]() ,
,![]() ,得
,得 ![]() ,
,
同理 ![]() ,
, ,
,
所以,直線 ![]() 的斜率為定值1.
的斜率為定值1.
【解析】(1)首先求出四邊形的面積,結合面積以及勾股定理公式得出當 | O P | 最小時, | A P | 就最小,,由題意可知最小距離即為原點到直線l的距離,求出該值即為四邊形面積的最小值。(2)首先根據題意由角的相等關系得出直線DM的斜率,再由點斜式求出直線的方程,聯立直線與圓的方程消元得到關于x的一元二次方程,結合韋達定理求出xMx1的值,因為xM的值為1進而求出x1的代數式,同理得到x2的代數式,故整理可得直線CD的斜率從而求出其值為1即可。
【考點精析】解答此題的關鍵在于理解直線的斜率的相關知識,掌握一條直線的傾斜角α(α≠90°)的正切值叫做這條直線的斜率,斜率常用小寫字母k表示,也就是 k = tanα.


科目:高中數學 來源: 題型:
【題目】如圖,在正方體ABCD-A1B1C1D1中,O為底面ABCD的中心,P是DD1的中點,設Q是CC1上的點,問:當點Q在什么位置時,平面D1BQ與平面PAO平行?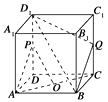
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖1所示,在直角梯形 ![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .將
.將 ![]() 沿
沿 ![]() 折起,使得點
折起,使得點 ![]() 在平面
在平面 ![]() 的正投影
的正投影 ![]() 恰好落在
恰好落在 ![]() 邊上,得到幾何體
邊上,得到幾何體 ![]() ,如圖2所示.
,如圖2所示.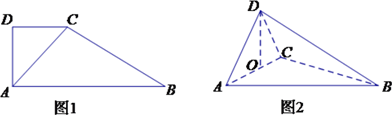
(1)求證: ![]() ;
;
(2)求點 ![]() 到平面
到平面 ![]() 的距離.
的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有一個正方體的玩具,六個面標注了數字1,2,3,4,5,6,甲、乙兩位學生進行如下游戲:甲先拋擲一次,記下正方體朝上的數字 ![]() ,再由乙拋擲一次,記下正方體朝上數字
,再由乙拋擲一次,記下正方體朝上數字 ![]() ,若
,若 ![]() 就稱甲、乙兩人“默契配合”,則甲、乙兩人“默契配合”的概率為( )
就稱甲、乙兩人“默契配合”,則甲、乙兩人“默契配合”的概率為( )
A.![]()
B.![]()
C.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在一個不透明的箱子里裝有5個完全相同的小球,球上分別標有數字1、2、3、4、5.甲先從箱子中摸出一個小球,記下球上所標數字后,將該小球放回箱子中搖勻后,乙再從該箱子中摸出一個小球.
(1)若甲、乙兩人誰摸出的球上標的數字大誰就獲勝(數字相同為平局),求甲獲勝的概率;
(2)規定:兩人摸到的球上所標數字之和小于6,則甲獲勝,否則乙獲勝,這樣規定公平嗎?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校在校學生2 000人,為了學生的“德、智、體”全面發展,學校舉行了跑步和登山比賽活動,每人都參加而且只參與其中一項比賽,各年級參與比賽的人數情況如下表:
高一年級 | 高二年級 | 高三年級 | |
跑步人數 | a | b | c |
登山人數 | x | y | z |
其中a∶b∶c=2∶5∶3,全校參與登山的人數占總人數的 ![]() .為了了解學生對本次活動的滿意程度,從中抽取一個200人的樣本進行調查,則高三年級參與跑步的學生中應抽取( )
.為了了解學生對本次活動的滿意程度,從中抽取一個200人的樣本進行調查,則高三年級參與跑步的學生中應抽取( )
A.15人
B.30人
C.40人
D.45人
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C: ![]() +
+ ![]() =1(a>b>0)的離心率為
=1(a>b>0)的離心率為 ![]() ,其左、右焦點為F1、F2 , 點P是坐標平面內一點,且|OP|=
,其左、右焦點為F1、F2 , 點P是坐標平面內一點,且|OP|= ![]() ,
, ![]()
![]() =
= ![]() ,其中O為坐標原點.
,其中O為坐標原點.
(1)求橢圓C的方程;
(2)如圖,過點S(0,﹣ ![]() )的動直線l交橢圓于A、B兩點,是否存在定點M,使以AB為直徑的圓恒過這個點?若存在,求出點M的坐標;若不存在,請說明理由.
)的動直線l交橢圓于A、B兩點,是否存在定點M,使以AB為直徑的圓恒過這個點?若存在,求出點M的坐標;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com