
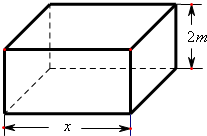
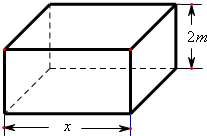
 現要求建造一個容積為8m3,深為2m的長方體無蓋水池(如圖),如果池底和池壁的造價分別為120元/m2和80元/m2.
現要求建造一個容積為8m3,深為2m的長方體無蓋水池(如圖),如果池底和池壁的造價分別為120元/m2和80元/m2.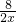 =
= m,
m, )×2=(4x+
)×2=(4x+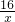 )(m2),S底=4(m2),
)(m2),S底=4(m2),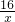 )+80×4=480x+
)+80×4=480x+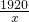 +320(元)(x>0).
+320(元)(x>0).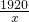 +320≥2
+320≥2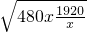 +320=960×2+320=2240(元).(當且僅當x=2時取“=”).
+320=960×2+320=2240(元).(當且僅當x=2時取“=”). m,利用池底和池壁的造價分別為120元/m2和80元/m2可求得函數解析式y=f(x)及x的取值范圍;
m,利用池底和池壁的造價分別為120元/m2和80元/m2可求得函數解析式y=f(x)及x的取值范圍;

 科學實驗活動冊系列答案
科學實驗活動冊系列答案科目:高中數學 來源: 題型:
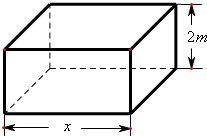 現要求建造一個容積為8m3,深為2m的長方體無蓋水池(如圖),如果池底和池壁的造價分別為120元/m2和80元/m2.
現要求建造一個容積為8m3,深為2m的長方體無蓋水池(如圖),如果池底和池壁的造價分別為120元/m2和80元/m2.查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com