
【題目】已知函數 ![]() 處都取得極值.
處都取得極值.
(1)求a,b的值;
(2)求f(x)的單調區間.
【答案】
(1)解:由已知可得f'(x)=3x2+2ax+b,
由 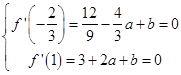
可得 ![]() ;
;
(2)解:由(1)知f'(x)=3x2﹣x﹣2=(3x+2)(x﹣1),
由 ![]() .列表如下:
.列表如下:
x |
|
|
| 1 | (1,+∞) |
f'(x) | + | 0 | ﹣ | 0 | + |
f(x) | 增 | 極大 | 減 | 極小 | 增 |
所以函數f(x)的遞增區間為 ![]() 與(1,+∞),遞減區間為
與(1,+∞),遞減區間為 ![]()
【解析】(1)求出函數的導數,得到關于a,b的方程組,解出即可求出a,b的值;(2)解關于導函數的不等式,從而求出函數的單調區間.
【考點精析】本題主要考查了利用導數研究函數的單調性和函數的極值與導數的相關知識點,需要掌握一般的,函數的單調性與其導數的正負有如下關系: 在某個區間![]() 內,(1)如果
內,(1)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞增;(2)如果
在這個區間單調遞增;(2)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞減;求函數
在這個區間單調遞減;求函數![]() 的極值的方法是:(1)如果在
的極值的方法是:(1)如果在![]() 附近的左側
附近的左側![]() ,右側
,右側![]() ,那么
,那么![]() 是極大值(2)如果在
是極大值(2)如果在![]() 附近的左側
附近的左側![]() ,右側
,右側![]() ,那么
,那么![]() 是極小值才能正確解答此題.
是極小值才能正確解答此題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】某農場共有土地50畝,這些地可種西瓜、棉花、玉米.這些農作物每畝地所需勞力和預計產值如下表.若該農場有20名勞動力,應怎樣計劃才能使每畝地都能種上作物(玉米必種),所有勞動力都被安排工作(每名勞動力只能種植一種作物)且作物預計總產值達最高?
作物 | 勞力/畝 | 產值/畝 |
西瓜 | 1/2 | 0.6萬元 |
棉花 | 1/3 | 0.5萬元 |
玉米 | 1/4 | 0.3萬元 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (
(![]() >0,
>0, ![]() ≠1,
≠1, ![]() ≠﹣1),是定義在(﹣1,1)上的奇函數.
≠﹣1),是定義在(﹣1,1)上的奇函數.
(1)求實數![]() 的值;
的值;
(2)當![]() =1時,判斷函數
=1時,判斷函數![]() 在(﹣1,1)上的單調性,并給出證明;
在(﹣1,1)上的單調性,并給出證明;
(3)若![]() 且
且![]() ,求實數
,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“累積凈化量(CCM)”是空氣凈化器質量的一個重要衡量指標,它是指空氣凈化器從開始使用到凈化效率為50%時對顆粒物的累積凈化量,以克表示.根據GB/T18801﹣2015《空氣凈化器》國家標準,對空氣凈化器的累積凈化量(CCM)有如下等級劃分:
累積凈化量(克) | (3,5] | (5,8] | (8,12] | 12以上 |
等級 | P1 | P2 | P3 | P4 |
為了了解一批空氣凈化器(共2000臺)的質量,隨機抽取n臺機器作為樣本進行估計,已知這n臺機器的
累積凈化量都分布在區間(4,14]中,按照(4,6],(6,8],(8,10],(10,12],(12,14],均勻分組,其中累積凈化量在(4,6]的所有數據有:4.5,4.6,5.2,5.7和5.9,并繪制了如下頻率分布直方圖.
(Ⅰ)求n的值及頻率分布直方圖中的x值;
(Ⅱ)以樣本估計總體,試估計這批空氣凈化器(共2000臺)中等級為P2的空氣凈化器有多少臺?
(Ⅲ)從累積凈化量在(4,6]的樣本中隨機抽取2臺,求恰好有1臺等級為P2的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數集X={x1,x2,…,xn}(其中xi>0,i=1,2,…,n,n≥3),若對任意的xk∈X(k=1,2,…,n),都存在xi,xj∈X(xi≠xj),使得下列三組向量中恰有一組共線:
①向量(xi,xk)與向量(xk,xj);②向量(xi,xj)與向量(xj,xk);③向量(xk,xi)與向量(xi,xj),則稱X具有性質P。例如{1,2,4}具有性質P。
(1)若{1,3,x)具有性質P,則x的取值為________;
(2)若數集{1,3,x1,x2}具有性質P,則x1+x2的最大值與最小值之積為________。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知命題p:x∈R,x+ ![]() ≥2;命題q:x0∈
≥2;命題q:x0∈ ![]() ,使sin x0+cos x0=
,使sin x0+cos x0= ![]() ,
,
則下列命題中為真命題的是( )
A.( ![]() p)∧q
p)∧q
B.p∧( ![]() q)
q)
C.( ![]() p)∧(
p)∧( ![]() q)
q)
D.p∧q
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com