解:(1)n=1時,a
1=S
1=a,
n≥2時,
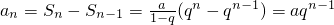
∵n=1時,a
1=a=aq
1-1也符合
∴
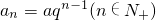
,可得
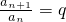
,即數列{a
n}是公比為q等比數列.
(2)設存在某一項,它能表示為另外三項之和,即
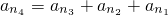
,
則
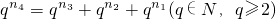
,
易得n
4是n
1、n
2、n
3、n
4中的最大值,不妨設n
4>n
3>n
2>n
1,
兩邊同除以
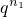
,整理得:
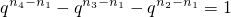
因為左邊能被q整除,右邊不能被q整除,因此滿足條件的q不存在.
∴不存在q的某些取值,使數列{a
n}中某一項能表示為另外三項之和
(3)若
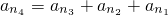
則
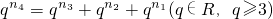
易得n
4是n
1、n
2、n
3、n
4中的最大值,不妨設n
4>n
3>n
2>n
1,
∵q≥3,

,
∴
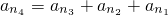
不成立.
因此,不存在q∈[3,+∞),使數列{a
n}中,某一項可以表示為另外三項之和.
分析:(1)利用公式a
n=
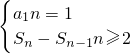
進行討論,然后綜合可得a
n的通項公式,從而證出數列{a
n}是公比為q等比數列.
(2)假設存在滿足條件的一項能表示為另外三項之和,設
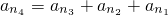
,經過討論可變形為
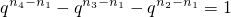
,根據等式兩邊對q的整除性,可知等式不成立,從而得到不存在滿足條件的q值.
(3)用類似(2)的方法,設
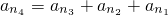
,結合{a
n}的通項公式和q≥3,利用不等式的性質證明出
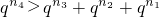
恒成立,從而證出等式不成立,從而得到不存在滿足條件的q值.
點評:本題給出等比數列,要我們探索能否存在一項使它等于另外三項的和,著重考查了等比數列的通項公式和不等式的基本性質等知識,屬于中檔題.

 .
.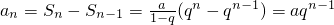
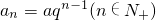 ,可得
,可得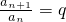 ,即數列{an}是公比為q等比數列.
,即數列{an}是公比為q等比數列.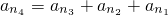 ,
,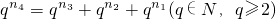 ,
,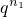 ,整理得:
,整理得: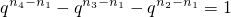
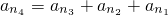 則
則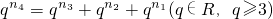
 ,
,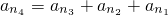 不成立.
不成立.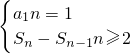 進行討論,然后綜合可得an的通項公式,從而證出數列{an}是公比為q等比數列.
進行討論,然后綜合可得an的通項公式,從而證出數列{an}是公比為q等比數列.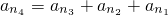 ,經過討論可變形為
,經過討論可變形為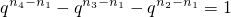 ,根據等式兩邊對q的整除性,可知等式不成立,從而得到不存在滿足條件的q值.
,根據等式兩邊對q的整除性,可知等式不成立,從而得到不存在滿足條件的q值.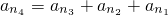 ,結合{an}的通項公式和q≥3,利用不等式的性質證明出
,結合{an}的通項公式和q≥3,利用不等式的性質證明出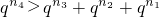 恒成立,從而證出等式不成立,從而得到不存在滿足條件的q值.
恒成立,從而證出等式不成立,從而得到不存在滿足條件的q值.

 字詞句段篇系列答案
字詞句段篇系列答案