
若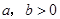 ,則
,則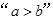 是“
是“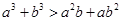 ”的( )
”的( )
A.充分非必要條件 B.必要非充分條件
C.充分且必要條件 D.既非充分也非必要條件
科目:高中數學 來源:2014屆浙江省高二下學期期中考試理科數學試卷(解析版) 題型:選擇題
有一段“三段論”推理是這樣的:對于可導函數 ,若
,若 ,則
,則 是函數
是函數 的極值點.因為
的極值點.因為 在
在 處的導數值
處的導數值 ,所以
,所以 是
是 的極值點. 以上推理中
的極值點. 以上推理中
A.大前提錯誤 B.小前提錯誤 C.推理形式錯誤 D.結論正確
查看答案和解析>>
科目:高中數學 來源:2013屆福建省高二下學期期中考試理科數學試卷(解析版) 題型:選擇題
下列說法正確的是
A.若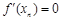 ,則
,則 是函數
是函數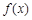 的極值
的極值
B.若 是函數
是函數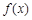 的極值,則
的極值,則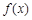 在
在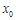 處有導數
處有導數
C.函數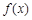 至多有一個極大值和一個極小值
至多有一個極大值和一個極小值
D.定義在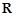 上的可導函數
上的可導函數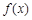 ,若方程
,若方程 無實數解,則
無實數解,則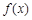 無極值
無極值
查看答案和解析>>
科目:高中數學 來源:遼寧省10-11學年高二下學期期末考試數學(理) 題型:解答題
(本小題滿分12分)(1)對于定義在 上的函數
上的函數 ,滿足
,滿足 ,求證:函數
,求證:函數 在
在 上是減函數;
上是減函數;
(2)請你認真研讀(1)中命題并聯系以下命題:若 是定義在
是定義在 上的可導函數,滿足
上的可導函數,滿足 ,則
,則 是
是 上的減函數。然后填空建立一個普遍化的命題:
上的減函數。然后填空建立一個普遍化的命題:
設 是定義在
是定義在 上的可導函數,
上的可導函數, ,若
,若  +
+
 ,
,
則
是 上的減函數。
上的減函數。
注:命題的普遍化就是從考慮一個對象過渡到考慮包含該對象的一個集合;或者從考慮一個較小的集合過渡到考慮包含該較小集合的更大集合。
(3)證明(2)中建立的普遍化命題。
查看答案和解析>>
科目:高中數學 來源:2010-2011年遼寧省高二下學期期末考試數學理科 題型:解答題
(本小題滿分12分)(1)對于定義在 上的函數
上的函數 ,滿足
,滿足 ,求證:函數
,求證:函數 在
在 上是減函數;
上是減函數;
(2)請你認真研讀(1)中命題并聯系以下命題:若 是定義在
是定義在 上的可導函數,滿足
上的可導函數,滿足 ,則
,則 是
是 上的減函數。然后填空建立一個普遍化的命題:
上的減函數。然后填空建立一個普遍化的命題:
設 是定義在
是定義在 上的可導函數,
上的可導函數, ,若
,若 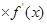 +
+
 ,
,
則
是 上的減函數。
上的減函數。
注:命題的普遍化就是從考慮一個對象過渡到考慮包含該對象的一個集合;或者從考慮一個較小的集合過渡到考慮包含該較小集合的更大集合。
(3)證明(2)中建立的普遍化命題。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com