
【題目】已知向量![]() ,設
,設![]() .
.
(1)求函數![]() 的解析式及單調遞增區間;
的解析式及單調遞增區間;
(2)在![]() 中,
中,![]() 分別為內角
分別為內角![]() 的對邊,且
的對邊,且![]() ,求
,求![]() 的面積.
的面積.
【答案】(1)[-![]() ]
]![]() ;(2)面積為
;(2)面積為 ![]() .
.
【解析】分析:(I)根據向量數量積的坐標公式得出f(x),利用二倍角公式,兩角和的正弦函數公式化簡,根據正弦函數的單調性得出f(x)的單調區間;
(II)根據f(A)=1和A的范圍解出A,利用余弦定理得出bc,代入面積公式S=![]() bcsinA即可.
bcsinA即可.
詳解:(I)f(x)=![]() sinxcosx+cos2x=
sinxcosx+cos2x=![]() sin2x+
sin2x+![]() cos2x+
cos2x+![]() =
=![]() .
.
![]() ,
,![]() .得[-
.得[-![]() ]
]![]() .
.
所以函數的單調遞增區間為[-![]() ]
]![]() .
.
(II)∵f(A)=sin(2A+![]() )+
)+![]() =1,∴sin(2A+
=1,∴sin(2A+![]() )=
)=![]() .
.
∵0<A<π,∴![]() <2A+
<2A+![]() <
<![]() ,∴2A+
,∴2A+![]() =
=![]() ,即A=
,即A=![]() .
.
由余弦定理得:a2=b2+c2﹣2bccosA=(b+c)2﹣2bc﹣2bccosA,∴1=4﹣3bc,∴bc=1.
∴![]() .
.


 同步練習強化拓展系列答案
同步練習強化拓展系列答案科目:高中數學 來源: 題型:
【題目】設![]() ,且f(x)=x有唯一解,
,且f(x)=x有唯一解,![]() ,xn+1=f(xn)(n∈N*).
,xn+1=f(xn)(n∈N*).
(1)求實數a的值;
(2)求數列{xn}的通項公式;
(3)若![]() ,數列b1,b2-b1,b3-b2,…,bn-bn-1是首項為1,公比為
,數列b1,b2-b1,b3-b2,…,bn-bn-1是首項為1,公比為![]() 的等比數列,記cn=anbn,求數列{cn}的前n項和Sn.
的等比數列,記cn=anbn,求數列{cn}的前n項和Sn.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=xln(1+x)﹣a(x+1),其中a為實常數.
(1)當x∈[1,+∞)時,f′(x)>0恒成立,求a的取值范圍;
(2)求函數 ![]() 的單調區間.
的單調區間.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在數列![]() 中,已知
中,已知![]() ,
,![]() (n∈N*)
(n∈N*)
(1)求數列![]() 的通項公式
的通項公式
(2)若![]() (λ為非零常數),問是否存在整數λ使得對任意n∈N*都有
(λ為非零常數),問是否存在整數λ使得對任意n∈N*都有![]() ?若存在,求出λ的值;若不存在,請說明理由.
?若存在,求出λ的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分![]() 分)
分)
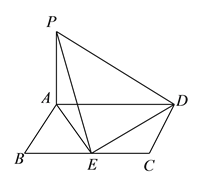
如圖,平行四邊形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,點
,點![]() 為
為![]() 中點,連結
中點,連結![]() 、
、![]() .
.
(Ⅰ)若![]() ,
, ![]() ,求證:平面
,求證:平面![]() 平面
平面![]() .
.
(Ⅱ)若![]() ,試探究在直線
,試探究在直線![]() 上有幾個點
上有幾個點![]() ,使得
,使得![]() ,并說明理由.
,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,直線
,直線![]() 與
與![]() 的圖象的相鄰兩個交點的橫坐標分別是
的圖象的相鄰兩個交點的橫坐標分別是![]() 和
和![]() ,現有如下命題:
,現有如下命題:
①該函數在![]() 上的值域是
上的值域是![]() ;
;
②在![]() 上,當且僅當
上,當且僅當![]() 時函數取最大值;
時函數取最大值;
③該函數的最小正周期可以是![]() ;
;
④![]() 的圖象可能過原點.
的圖象可能過原點.
其中的真命題有__________.(寫出所有真命題的序號)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校進行體驗,現得到所有男生的身高數據,從中隨機抽取50人進行統計(已知這50個身高介于155 ![]() 到195
到195![]() 之間),現將抽取結果按如下方式分成八組:第一組
之間),現將抽取結果按如下方式分成八組:第一組![]() ,第二組
,第二組![]() ,…,第八組
,…,第八組![]() ,并按此分組繪制如圖所示的頻率分布直方圖,其中第六組
,并按此分組繪制如圖所示的頻率分布直方圖,其中第六組![]() 和第七組
和第七組![]() 還沒有繪制完成,已知第一組與第八組人數相同,第六組和第七組人數的比為5:2.
還沒有繪制完成,已知第一組與第八組人數相同,第六組和第七組人數的比為5:2.
(1)補全頻率分布直方圖;
(2)根據頻率分布直方圖估計這50位男生身高的中位數;
(3)用分層抽樣的方法在身高為![]() 內抽取一個容量為5的樣本,從樣本中任意抽取2位男生,求這兩位男生身高都在
內抽取一個容量為5的樣本,從樣本中任意抽取2位男生,求這兩位男生身高都在![]() 內的概率.
內的概率.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com