
【題目】已知函數 ![]() .
.
(1)作出函數y=f(x)在一個周期內的圖象,并寫出其單調遞減區間;
(2)當 ![]() 時,求f(x)的最大值與最小值.
時,求f(x)的最大值與最小值.
 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】△ABC的內角A,B,C的對邊分別為a,b,c,其中b≠c,且bcosB=ccosC,延長線段BC到點D,使得BC=4CD=4,∠CAD=30°, 
(Ⅰ)求證:∠BAC是直角;
(Ⅱ)求tan∠D的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知隨圓E: ![]() +
+ ![]() =1(a>b>0)與過原點的直線交于A、B兩點,右焦點為F,∠AFB=120°,若△AFB的面積為4
=1(a>b>0)與過原點的直線交于A、B兩點,右焦點為F,∠AFB=120°,若△AFB的面積為4 ![]() ,則橢圓E的焦距的取值范圍是( )
,則橢圓E的焦距的取值范圍是( )
A.[2,+∞)
B.[4,+∞)
C.[2 ![]() ,+∞)
,+∞)
D.[4 ![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=xlnx,g(x)=x+ ![]() (x>0)都在x=x0處取得最小值.
(x>0)都在x=x0處取得最小值.
(1)求f(x0)﹣g(x0)的值.
(2)設函數h(x)=f(x)﹣g(x),h(x)的極值點之和落在區間(k,k+1),k∈N,求k的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】方程為x2+y2﹣4x﹣2y+4=0.以O為極點,x軸正半軸為極軸建立極坐標系.
(1)求l的普通方程與C的極坐標方程;
(2)已知l與C交于P,Q,求|PQ|.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設圓 ![]() 的圓心為F1 , 直線l過點F2(2,0)且不與x軸、y軸垂直,且與圓F1于C,D兩點,過F2作F1C的平行線交直線F1D于點E,
的圓心為F1 , 直線l過點F2(2,0)且不與x軸、y軸垂直,且與圓F1于C,D兩點,過F2作F1C的平行線交直線F1D于點E,
(1)證明||EF1|﹣|EF2||為定值,并寫出點E的軌跡方程;
(2)設點E的軌跡為曲線Γ,直線l交Γ于M,N兩點,過F2且與l垂直的直線與圓F1交于P,Q兩點,求△PQM與△PQN的面積之和的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】北京市2016年12個月的PM2.5平均濃度指數如圖所示.由圖判斷,四個季度中PM2.5的平均濃度指數方差最小的是( ) 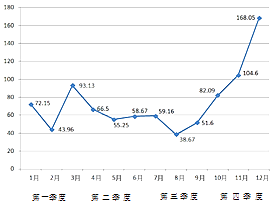
A.第一季度
B.第二季度
C.第三季度
D.第四季度
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,A、B、C的對邊分別為a,b,c,已知A≠ ![]() ,且3sinAcosB+
,且3sinAcosB+ ![]() bsin2A=3sinC.
bsin2A=3sinC.
(I)求a的值;
(Ⅱ)若A= ![]() ,求△ABC周長的最大值.
,求△ABC周長的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com