
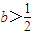 時,判斷函數f(x)在定義域上的單調性;
時,判斷函數f(x)在定義域上的單調性;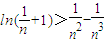 都成立.
都成立. ,0<b<
,0<b< ,b≤0或f'(x)<0.參數取某些特定值時,可只管作出判斷,單列為一類;不能作出直觀判斷的,再分為一類,用通法解決,另外要注意由f'(x)=0求得的根不一定就是極值點,需要判斷在該點兩側的異號性后才能稱為“極值點”.
,b≤0或f'(x)<0.參數取某些特定值時,可只管作出判斷,單列為一類;不能作出直觀判斷的,再分為一類,用通法解決,另外要注意由f'(x)=0求得的根不一定就是極值點,需要判斷在該點兩側的異號性后才能稱為“極值點”.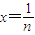 ,即可證得結論.
,即可證得結論.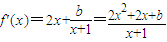
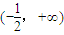 上遞增,在
上遞增,在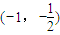 上遞減,
上遞減,
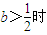 ,函數f(x)在定義域(-1,+∞)上單調遞增.
,函數f(x)在定義域(-1,+∞)上單調遞增.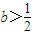 時函數f(x)無極值點
時函數f(x)無極值點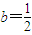 時,
時,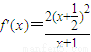 ,
,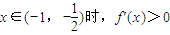
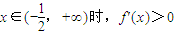 ,
,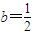 時,函數f(x)在(-1,+∞)上無極值點
時,函數f(x)在(-1,+∞)上無極值點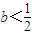 時,解f'(x)=0得兩個不同解
時,解f'(x)=0得兩個不同解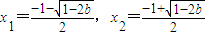
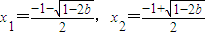 ,
,
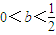 時,x1,x2∈(-1,+∞)f'(x)在(-1,x1),(x2,+∞)都大于0,
時,x1,x2∈(-1,+∞)f'(x)在(-1,x1),(x2,+∞)都大于0, 和一個極小值點
和一個極小值點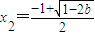
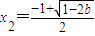
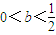 時,f(x)有一個極大值點
時,f(x)有一個極大值點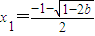 和一個極小值點
和一個極小值點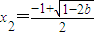
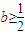 時,函數f(x)在(-1,+∞)上無極值點.
時,函數f(x)在(-1,+∞)上無極值點.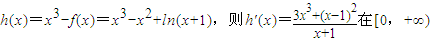 上恒正
上恒正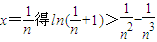


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
| 1 | x+1 |
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
| n+1 |
| n |
| n-1 |
| n3 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com