
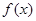 的定義域為R,當
的定義域為R,當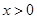 時,
時,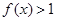 ,且對任意
,且對任意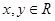 ,都有
,都有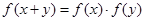 ,且
,且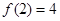 。
。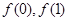 的值;
的值;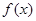 在R上為單調遞增函數;
在R上為單調遞增函數;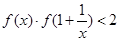 成立,求
成立,求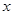 的取值范圍。
的取值范圍。 ,
,  ;(2)
;(2)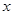 的取值范圍是
的取值范圍是 。
。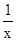 )<f(1),再利用函數的單調性將不等式轉化為分式不等式即可得解集。
)<f(1),再利用函數的單調性將不等式轉化為分式不等式即可得解集。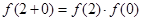 ,所以
,所以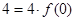 ,所以
,所以 ,又因為
,又因為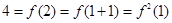 ,且當
,且當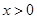 時,
時,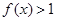 ,所以
,所以
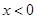 時,
時,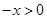 ,所以
,所以 ,而
,而 ,所以
,所以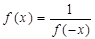 ,所以
,所以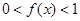 ,對任意的
,對任意的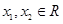 ,當
,當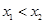 時,有
時,有

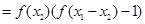 ,因為
,因為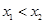 ,所以
,所以 ,所以
,所以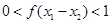 ,即
,即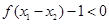 ,所以
,所以 ,即
,即 ,所以
,所以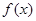 在R上是單調遞增函數(3)因為
在R上是單調遞增函數(3)因為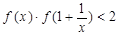 ,所以
,所以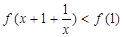 ,而
,而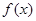 在R上是單調遞增函數,所以
在R上是單調遞增函數,所以 ,即:
,即: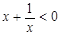 ,所以
,所以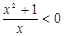 ,所以
,所以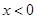 ,所以
,所以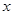 的取值范圍是
的取值范圍是


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源:不詳 題型:解答題
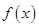 是定義在
是定義在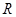 上單調函數,對任意實數
上單調函數,對任意實數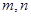 有:
有: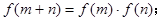 且
且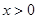 時,
時,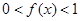 .
.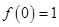 ;
;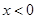 時,
時,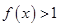 ;
;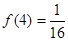 時,求使
時,求使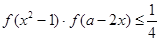 對任意實數
對任意實數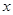 恒成立的參數
恒成立的參數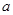 的取值范圍.
的取值范圍.查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
 在
在 上是增函數,且最小值是1,則它在
上是增函數,且最小值是1,則它在 上是( )
上是( )| A.增函數且最小值是-1 | B.增函數且最大值是-1 |
| C.減函數且最大值是-1 | D.減函數且最小值是-1 |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
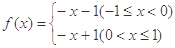 ,則
,則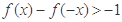 的解集為( )
的解集為( )| A.(-∞,-1)∪(1,+∞) | B.[-1,- )∪(0,1] )∪(0,1] |
| C.(-∞,0)∪(1,+∞) | D.[-1,- ]∪(0,1) ]∪(0,1) |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
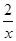 ;④f(x)=
;④f(x)=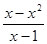 .
.| A.0 | B.1 | C.2 | D.3 |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
| A.[-2,2] | B.[-1,2] |
C.[-1,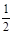 ) ) | D.[-1,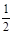 ] ] |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com