
【題目】已知函數f(x)=|lgx|.若a≠b且,f(a)=f(b),則a+b的取值范圍是( )
A.(1,+∞)
B.[1,+∞)
C.(2,+∞)
D.[2,+∞)
【答案】C
【解析】解:(方法一)因為f(a)=f(b),所以|lga|=|lgb|,
不妨設0<a<b,則0<a<1<b,∴lga=﹣lgb,lga+lgb=0
∴lg(ab)=0
∴ab=1,
又a>0,b>0,且a≠b
∴(a+b)2>4ab=4
∴a+b>2
故選:C.
(方法二)由對數的定義域,設0<a<b,且f(a)=f(b),得: 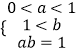 ,
,
整理得線性規劃表達式為: 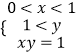 ,
,
因此問題轉化為求z=x+y的取值范圍問題,則z=x+yy=﹣x+z,即求函數的截距最值.
根據導數定義, ![]() 函數圖象過點(1,1)時z有最小為2(因為是開區域,所以取不到2),
函數圖象過點(1,1)時z有最小為2(因為是開區域,所以取不到2),
∴a+b的取值范圍是(2,+∞).
故選:C.
【考點精析】認真審題,首先需要了解函數的值域(求函數值域的方法和求函數最值的常用方法基本上是相同的.事實上,如果在函數的值域中存在一個最小(大)數,這個數就是函數的最小(大)值.因此求函數的最值與值域,其實質是相同的),還要掌握對數函數的單調性與特殊點(過定點(1,0),即x=1時,y=0;a>1時在(0,+∞)上是增函數;0>a>1時在(0,+∞)上是減函數)的相關知識才是答題的關鍵.


 數學奧賽暑假天天練南京大學出版社系列答案
數學奧賽暑假天天練南京大學出版社系列答案科目:高中數學 來源: 題型:
【題目】某研究所計劃利用“神七”宇宙飛船進行新產品搭載實驗,計劃搭載新產品A、B,要根據該產品的研制成本、產品重量、搭載實驗費用和預計產生收益來決定具體安排,通過調查,有關數據如表:
產品A(件) | 產品B(件) | ||
研制成本、搭載費用之和(萬元) | 20 | 30 | 計劃最大資金額300萬元 |
產品重量(千克) | 10 | 5 | 最大搭載重量110千克 |
預計收益(萬元) | 80 | 60 |
試問:如何安排這兩種產品的件數進行搭載,才能使總預計收益達到最大,最大收益是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】命題P:將函數sin2x的圖象向右平移 ![]() 個單位得到函數y=sin(2x﹣
個單位得到函數y=sin(2x﹣ ![]() )的圖象;命題Q:函數y=sin(x+
)的圖象;命題Q:函數y=sin(x+ ![]() )cos(
)cos( ![]() ﹣x)的最小正周期是π,則復合命題“P或Q”“P且Q”“非P”為真命題的個數是個.
﹣x)的最小正周期是π,則復合命題“P或Q”“P且Q”“非P”為真命題的個數是個.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】小王在年初用50萬元購買一輛大貨車,第一年因繳納各種費用需支出6萬元,從第二年起,每年都比上一年增加支出2萬元,假定該車每年的運輸收入均為25萬元.小王在該車運輸累計收入超過總支出后,考慮將大貨車作為二手車出售,若該車在第x年年底出售,其銷售價格為25-x萬元(國家規定大貨車的報廢年限為10年).
(1)大貨車運輸到第幾年年底,該車運輸累計收入超過總支出?
(2)在第幾年年底將大貨車出售,能使小王獲得的年平均利潤最大(利潤=累計收入+銷售收入-總支出)?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校數學課外興趣小組為研究數學成績是否與性別有關,先統計本校高三年級每個學生一學期數學成績平均分(采用百分制),剔除平均分在30分以下的學生后,共有男生300名,女生200名.現采用分層抽樣的方法,從中抽取了100名學生,按性別分為兩組,并將兩組學生成績分為6組,得到如下所示頻數分布表.
分數段 | [40,50) | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
男 | 3 | 9 | 18 | 15 | 6 | 9 |
女 | 6 | 4 | 5 | 10 | 13 | 2 |
(I)估計男、女生各自的平均分(同一組數據用該組區間中點值作代表),從計算結果看,能否判斷數學成績與性別有關;
(II)規定80分以上為優分(含80分),請你根據已知條件完成2×2列聯表,并判斷是否有90%以上的把握認為“數學成績與性別有關”. ( ,其中
,其中![]() )
)

查看答案和解析>>
科目:高中數學 來源: 題型:
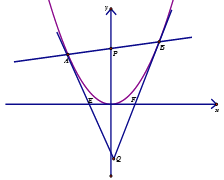
【題目】已知拋物線C: ![]() ,過點
,過點![]() 的動直線l與C相交于
的動直線l與C相交于![]() 兩點,拋物線C在點A和點B處的切線相交于點Q.
兩點,拋物線C在點A和點B處的切線相交于點Q.
(Ⅰ)寫出拋物線的焦點坐標和準線方程;
(Ⅱ)求證:點Q在直線![]() 上;
上;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合M={1,2,3,4},N={(a,b)|a∈M,b∈M},A是集合N中任意一點,O為坐標原點,則直線OA與y=x2+1有交點的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com