
【題目】已知函數(shù)f(x)=mx3+x﹣sinx(m∈R).
(1)當m=0時,(i)求y=f(x)在(![]() ,f(
,f(![]() ))處的切線方程;
))處的切線方程;
(ii)證明:f(x)<ex;
(2)當x≥0時,函數(shù)f(x)單調遞減,求m的取值范圍.
【答案】(1)(i)![]() (ii)見解析(2)
(ii)見解析(2)![]()
【解析】
(1)(i) 根據(jù)導數(shù)的幾何意義求出切線斜率,由點斜式即可得結果;(ii ) 當![]() 時,原命題等價于
時,原命題等價于![]() ,結合
,結合![]() ,即證
,即證![]() ,令
,令![]() ,利用異數(shù)研究其單調性,可得
,利用異數(shù)研究其單調性,可得![]() ,從而可得結論;(2)依題意
,從而可得結論;(2)依題意![]() 在
在![]() 上恒成立,令
上恒成立,令![]() ,求導
,求導![]() ,令
,令![]() ,利用導數(shù)研究其單調性可,通過對
,利用導數(shù)研究其單調性可,通過對![]() 分類討論,即可篩選出符合題意的
分類討論,即可篩選出符合題意的![]() 取值范圍.
取值范圍.
(1)當![]() 時,
時,![]() .
.
(i)![]() ,
,![]() ,
,
![]() ,
,
![]() 在
在![]() 處的切線方程為
處的切線方程為![]() ,
,
即![]() .
.
(ii)原命題等價于![]() ,
,
![]() ,即證
,即證![]() ,
,
令![]() ,則
,則![]() ,
,
當![]() 時,
時,![]() 單調遞增;
單調遞增;
當![]() 時,
時,![]() 單調遞減,
單調遞減,
![]() ,
,
![]() ,取等號條件不一致,
,取等號條件不一致,
![]() ,
,
![]() .
.
(2)依題意,![]() 在
在![]() 時恒成立,
時恒成立,
令![]() ,則
,則![]() ,
,
當![]() 時,
時,![]() ,
,![]() .
.
(i)當![]() 時,
時,![]() 單調遞減,
單調遞減,
![]() ,即
,即![]() ,符合題意.
,符合題意.
(ii)當![]() 時,
時,![]() ,不符合題意,舍去.
,不符合題意,舍去.
(iii)當![]() 時,令
時,令![]() ,則
,則![]() ,
,
由![]() ,
,
![]() ,
,
![]() ,使
,使![]() ,
,
所以當![]() 時,
時,![]() 在
在![]() 單調遞增,
單調遞增,
所以當![]() 時,
時,![]() ,即
,即![]() ,
,
所以當![]() 時,
時,![]() 在
在![]() 上單調遞增,
上單調遞增,
![]() ,即
,即![]() ,不符合題意,舍去,
,不符合題意,舍去,
故![]() .
.


 寒假樂園北京教育出版社系列答案
寒假樂園北京教育出版社系列答案科目:高中數(shù)學 來源: 題型:
【題目】如圖所示,直角梯形公園![]() 中,
中,![]() ,
,![]() ,
,![]() ,公園的左下角陰影部分為以
,公園的左下角陰影部分為以![]() 為圓心,半徑為
為圓心,半徑為![]() 的
的![]() 圓面的人工湖,現(xiàn)設計修建一條與圓相切的觀光道路
圓面的人工湖,現(xiàn)設計修建一條與圓相切的觀光道路![]() (點
(點![]() 分別在
分別在![]() 與
與![]() 上),
上),![]() 為切點,設
為切點,設![]() .
.

(1)試求觀光道路![]() 長度的最大值;
長度的最大值;
(2)公園計劃在道路![]() 的右側種植草坪,試求草坪
的右側種植草坪,試求草坪![]() 的面積最大值.
的面積最大值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】為調查某地區(qū)老年人是否需要志愿者提供幫助,用簡單隨機抽樣的方法從該地區(qū)調查了500位老年人,結果如下:
性別 是否需要志愿者 | 男 | 女 |
需要 | 40 | 30 |
不需要 | 160 | 270 |
附:![]() 的觀測值
的觀測值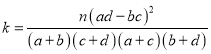
| 0.05 | 0.01 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(1)估計該地區(qū)老年人中,需要志愿者提供幫助的老年人的比例;
(2)在犯錯誤的概率不超過0.01的前提下是否可認為該地區(qū)的老年人是否需要志愿者提供幫助與性別有關?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)f(x)=sin(2x+![]() )+cos(2x﹣
)+cos(2x﹣![]() )+cos2x﹣sin2x,x∈R.
)+cos2x﹣sin2x,x∈R.
(1)求函數(shù)f(x)的最小正周期及單調遞增區(qū)間;
(2)求函數(shù)f(x)在區(qū)間[﹣![]() ]上的最大值和最小值.
]上的最大值和最小值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)f(x)=sin(![]() )的圖象與函數(shù)g(x)的圖象關于x=1對稱,則函數(shù)g(x)在(﹣6,﹣4)上( )
)的圖象與函數(shù)g(x)的圖象關于x=1對稱,則函數(shù)g(x)在(﹣6,﹣4)上( )
A. 單調遞增 B. 單調遞減 C. 先增后減 D. 先減后增
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知平面四邊形MNPQ中,MN=![]() ,MP=1,MP⊥MN,PQ⊥QM.
,MP=1,MP⊥MN,PQ⊥QM.
(Ⅰ)若PQ=![]() ,求NQ的值;
,求NQ的值;
(Ⅱ)若∠MQN=30°,求sin∠QMP的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
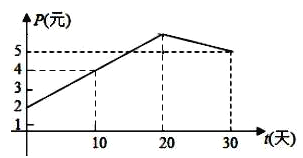
【題目】某上市股票在30天內每股的交易價格P(元)與時間t(天)組成有序數(shù)對![]() ,點
,點![]() 落在如圖所示的兩條線段上.該股票在30天內(包括30天)的日交易量M(萬股)與時間t(天)的部分數(shù)據(jù)如下表所示:
落在如圖所示的兩條線段上.該股票在30天內(包括30天)的日交易量M(萬股)與時間t(天)的部分數(shù)據(jù)如下表所示:
第t天 | 6 | 13 | 20 | 27 |
M(萬股) | 34 | 27 | 20 | 13 |
(1)根據(jù)提供的圖象,寫出該股票每股交易價格P(元)與時間t(天)所滿足的函數(shù)關系式![]() ______;
______;
(2)根據(jù)表中數(shù)據(jù),寫出日交易量M(萬股)與時間t(天)的一次函數(shù)關系式:![]() ______;
______;
(3)用y(萬元)表示該股票日交易額,寫出y關于t的函數(shù)關系式,并求在這30天內第幾天日交易額最大,最大值為多少?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知以點P為圓心的圓經(jīng)過點A(-1,0)和B(3,4),線段AB的垂直平分線交圓P于點C和D,且|CD|=![]() .
.
(1)求直線CD的方程;
(2)求圓P的方程.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com