【題目】某企業生產某種商品
噸，此時所需生產費用為（
）萬元，當出售這種商品時，每噸價格為
萬元，這里
（
為常數，
）
（1）為了使這種商品的生產費用平均每噸最低，那么這種商品的產量應為多少噸？
（2）如果生產出來的商品能全部賣完，當產量是120噸時企業利潤最大，此時出售價格是每噸160萬元，求的值．
【答案】（1）100噸；（2）
．
【解析】
試題這是函數應用題問題，解決問題的方法是列出函數關系式，然后借助函數的性質得出結論．這種問題的函數式其實在題中已經有提示，我們只要充分利用題目提供的信息，就可以得到解法．顯然本題要建立生產商品的平均費用與商品產量之間的函數式，已知條件是生產某種商品
噸，此時所需生產費用為（
）萬元，因此平均費用就是
，這就是所求函數式；（2）當產量是120噸時企業利潤最大，解決這個問題要建立利潤與產量之間的函數式，從實際出發，我們知道利潤等于收入減去成本，因此此題中利潤
，這是關于的二次函數，已知條件轉化為當
時，
最大，且此時銷售單價
，故問題得解．
試題解析：（1）設生產平均費用為y元，（1分）
由題意可知y=
;（5分）
當且僅當
時等號成立，（6分）
所以這種商品的產量應為100噸．（7分）
（2）設企業的利潤為S元，有題意可知（7分）
=
（3分）
又由題意可知120
（5分）
（6分）
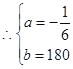（7分）
名校課堂系列答案科目：高中數學 來源： 題型：
【題目】下列有關命題的說法錯誤的是（ ）
A. 若“
”為假命題，則p，q均為假命題
B. “ 
”是“
”的充分不必要條件
C. “
”的必要不充分條件是“
”
D. 若命題p：
，
，則命題
：
，
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列有關命題的說法中錯誤的是( )
A. 若
為真命題，則
中至少有一個為真命題.
B. 命題：“若
是冪函數，則的圖象不經過第四象限”的否命題是假命題.
C. 命題“
，有
且
”的否定形式是“
，有
且
”.
D. 若直線
和平面
，滿足
.則“
” 是“
”的充分不必要條件.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，梯形ABCD所在的平面與等腰梯形ABEF所在的平面互相垂直，AB∥CD∥EF，AB⊥AD，CD＝DA＝AF＝FE＝2，AB＝4.
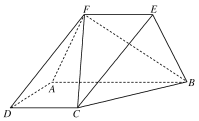
(1)求證：DF∥平面BCE；
(2)求二面角C—BF—A的正弦值；
(3)線段CE上是否存在點G，使得AG⊥平面BCF？請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知定點M(0,2)，N(－2,0)，直線l：kx－y－2k＋2＝0(k為常數)．
(1)若點M，N到直線l的距離相等，求實數k的值；
(2)對于l上任意一點P，∠MPN恒為銳角，求實數k的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】總體由編號為01，02，…，49，50的50個個體組成，利用下面的隨機數表選取6個個體，選取方法是從隨機數表第7行的第9列和第10列數字開始從左到右依次選取兩個數字，則選出的第4個個體的編號為（ ）
附：第6行至第8行的隨機數表
2748 6198 7164 4148 7086 2888 8519 1620 7477
0111 1630 2404 2979 7991 9624 5125 3211 4919
7306 4916 7677 8733 9974 6732 2635 7900 3370
A.11B.24C.25D.20
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設y＝f(x)在(－∞，1]上有定義，對于給定的實數K，定義fK(x)＝
，給出函數f(x)＝2x＋1－4x，若對于任意x∈(－∞，1]，恒有fK(x)＝f(x)，則( )
A.K的最大值為0
B.K的最小值為0
C.K的最大值為1
D.K的最小值為1
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設函數f（x）＝|x﹣a|+3x，其中a＞0．
（1）當a＝1時，求不等式f（x）＞3x+2的解集；
（2）若不等式f（x）≤0的解集為{x|x≤﹣1}，求a的值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
