
設三次函數h(x)=px3+qx2+rx+s滿足下列條件:h(1)=1,h(-1)= -1,在區間(-1,1)上分別取得極大值1和極小值-1,對應的極點分別為a,b。
(1)證明:a+b=0
(2)求h(x)的表達式
(3)已知三次函數f(x)=ax3+bx2+cx+d在(-1,1)上滿足-1<f(x)<1。證明當|x|>1時,有|f(x)|<|h(x)|
(1)見解析(2)h(x)=4x3-3x(3)見解析
(1)解:由f(1)=1,f(-1)=-1得q+s=0,r+p=1
h(x)=px3-sx2+(1-p)x+s
h’(x)=3px2-2sx+1-p
因為(-1,1)內有兩極值且f(1)=1,所以有p>0
![]() =0(*)
=0(*)
又由韋達定理得![]() ,即
,即![]() 代入(*)中得
代入(*)中得
![]()
因為p>0,a+b??(-2,2),所以![]()
所以有![]()
(2)解:由![]() 得s=0,q=0
得s=0,q=0
所以h(x)=px3+(1-p)x,又![]()
消去p得![]() 所以有
所以有![]()
所以有h(x)=4x3-3x
(3)解:因為|x|<1時|f(x)|<1,所以有|f(1)|??1,|f(-1)|??1
令F(x)=h(x)+f(x),G(x)=h(x)-f(x)
則有F(1)=1+f(1)??0,F(![]() )=-1+f(
)=-1+f(![]() )<0,F(
)<0,F(![]() )=1+f(-
)=1+f(-![]() )>0,F(-1)=-1+f(-1)??0
)>0,F(-1)=-1+f(-1)??0
所以有F(x)在(-1,1)內有極大值和極小值,當x>1時,F(x)>0,當x<-1時,F(x)<0
同理有:G(1)=1-f(1)??0, G(![]() )=-1-f(
)=-1-f(![]() )<0, G(
)<0, G(![]() )=1-f(-
)=1-f(-![]() )>0,
)>0,
G(-1)=-1-f(-1)??0
所以有G(x)在(-1,1)內有極大值和極小值,當x>1時,G(x)>0,當x<-1時,G(x)<0
所以當|x|>1時,有F(x)G(x)>0即h2(x)>f2(x)即|h(x)|>|f(x)


科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
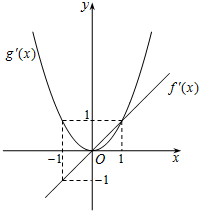 (2013•武漢模擬)已知函數f'(x)、g'(x)分別是二次函數f(x)和三次函數g(x)的導函數,它們在同一坐標系下的圖象如圖所示:
(2013•武漢模擬)已知函數f'(x)、g'(x)分別是二次函數f(x)和三次函數g(x)的導函數,它們在同一坐標系下的圖象如圖所示:查看答案和解析>>
科目:高中數學 來源:2010年江西省九江市都昌二中高考數學模擬試卷(文科)(解析版) 題型:解答題
查看答案和解析>>
科目:高中數學 來源:0107 模擬題 題型:填空題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com