
【題目】如圖所示,等腰![]() 的底邊
的底邊![]() ,高
,高![]() ,點
,點![]() 是線段
是線段![]() 上異于點
上異于點![]() 的動點,點
的動點,點![]() 在
在![]() 邊上,且
邊上,且![]() ,現沿
,現沿![]() 將△
將△![]() 折起到△
折起到△![]() 的位置,使
的位置,使![]() ,記
,記![]() ,
, ![]() 表示四棱錐
表示四棱錐![]() 的體積.
的體積.
(1)求![]() 的表達式;(2)當
的表達式;(2)當![]() 為何值時,
為何值時, ![]() 取得最大,并求最大值。
取得最大,并求最大值。
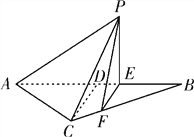
【答案】(1) VP-ACFE=![]() (2)
(2) ![]()
![]()
【解析】試題分析:(1)![]() ,S四邊形ACFE=S△ABC-S△BEF=
,S四邊形ACFE=S△ABC-S△BEF=![]() ,所以四棱錐P-ACFE的體積VP-ACFE=
,所以四棱錐P-ACFE的體積VP-ACFE=![]() S四邊形ACFE·PE=
S四邊形ACFE·PE=![]() ;(2)V′(x)=0
;(2)V′(x)=0 ![]() ,所以
,所以![]()
![]() 。
。
試題解析:
(1)因為EF⊥AB,所以EF⊥PE.又因為PE⊥AE,EF∩AE=E,所以PE⊥平面ACFE. 因為EF⊥AB,CD⊥AB,且CD,EF共面,所以EF∥CD,
所以![]()
![]()
所以四邊形ACFE的面積
S四邊形ACFE=S△ABC-S△BEF=![]()
所以四棱錐P-ACFE的體積VP-ACFE=![]() S四邊形ACFE·PE=
S四邊形ACFE·PE=![]()
(2)由(1)知. ![]() 令V′(x)=0
令V′(x)=0 ![]() 因為當
因為當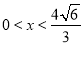 時,V′(x)>0, 當
時,V′(x)>0, 當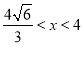 時,V′(x)<0.所以當
時,V′(x)<0.所以當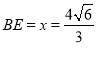 時,
時, 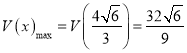


科目:高中數學 來源: 題型:
【題目】已知![]() 被直線
被直線![]() ,
, ![]() 分成面積相等的四個部分,且截
分成面積相等的四個部分,且截![]() 軸所得線段的長為2.
軸所得線段的長為2.
(1)求![]() 的方程;
的方程;
(2)若存在過點![]() 的直線與
的直線與![]() 相交于
相交于![]() ,
, ![]() 兩點,且點
兩點,且點![]() 恰好是線段
恰好是線段![]() 的中點,求實數
的中點,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某家電公司銷售部門共有200位銷售員,每位部門對每位銷售員都有1400萬元的年度銷售任務,已知這200位銷售員去年完成銷售額都在區間![]() (單位:百萬元)內,現將其分成5組,第1組,第2組,第3組,第4組,第5組對應的區間分別為
(單位:百萬元)內,現將其分成5組,第1組,第2組,第3組,第4組,第5組對應的區間分別為![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,繪制出頻率分布直方圖.
,繪制出頻率分布直方圖.

(1)求![]() 的值,并計算完成年度任務的人數;
的值,并計算完成年度任務的人數;
(2)用分層抽樣從這200位銷售員中抽取容量為25的樣本,求這5組分別應抽取的人數;
(3)現從(2)中完成年度任務的銷售員中隨機選取2位,獎勵海南三亞三日游,求獲得此獎勵的2位銷售員在同一組的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]()
(1)若函數![]() 在區間[0,1]上存在零點,求實數
在區間[0,1]上存在零點,求實數![]() 的取值范圍;
的取值范圍;
(2)當![]() 時,若對任意
時,若對任意![]() ∈[0,4],總存在
∈[0,4],總存在![]() ∈[0,4],使
∈[0,4],使![]() 成立,求實數
成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《算法統宗》是中國古代數學名著,由明代數學家程大位編著. 《算法統宗》對我國民間普及珠算和數學知識起到了很大的作用,是東方古代數學的名著.在這部著作中,許多數學問題都是以歌訣形式呈現的,以“竹筒容米”就是其中一首:家有九節竹一莖,為因盛米不均平;下頭三節三升九,上梢四節貯三升;唯有中間二節竹,要將米數次第盛;若是先生能算法,也教算得到天明!大意是:用一根9節長的竹子盛米,每節竹筒盛米的容積是不均勻的.下端3節可盛米3.9升,上端4節可盛米3升,要按每節依次盛容積相差同一數量的方式盛米,中間兩節可盛米多少升?由以上條件,計算出中間兩節的容積為( )
A. ![]() 升 B.
升 B. ![]() 升 C.
升 C. ![]() 升 D.
升 D. ![]() 升
升
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】光線從點A(-3,4)射出,到x軸上的點B后,被x軸反射到y軸上的點C,又被y軸反射,這時反射光線恰好過點D(-1,6),求光線BC所在直線的斜率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com