
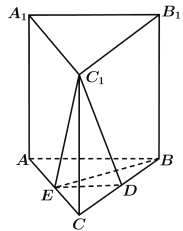
【題目】如圖,在直三棱柱ABC-A1B1C1中,D,E分別為BC,AC的中點,AB=BC.

求證:(1)A1B1∥平面DEC1;
(2)BE⊥C1E.
【答案】(1)見解析;(2)見解析.
【解析】
(1)由題意結合幾何體的空間結構特征和線面平行的判定定理即可證得題中的結論;
(2)由題意首先證得線面垂直,然后結合線面垂直證明線線垂直即可.
(1)因為D,E分別為BC,AC的中點,
所以ED∥AB.
在直三棱柱ABC-A1B1C1中,AB∥A1B1,
所以A1B1∥ED.
又因為ED平面DEC1,A1B1![]() 平面DEC1,
平面DEC1,
所以A1B1∥平面DEC1.
(2)因為AB=BC,E為AC的中點,所以BE⊥AC.
因為三棱柱ABC-A1B1C1是直棱柱,所以CC1⊥平面ABC.
又因為BE平面ABC,所以CC1⊥BE.
因為C1C平面A1ACC1,AC平面A1ACC1,C1C∩AC=C,
所以BE⊥平面A1ACC1.
因為C1E平面A1ACC1,所以BE⊥C1E.


科目:高中數學 來源: 題型:
【題目】已知數列![]() ,
,![]() ,其前
,其前![]() 項和
項和![]() 滿足
滿足![]() ,其中
,其中![]() .
.
(1)設![]() ,證明:數列
,證明:數列![]() 是等差數列;
是等差數列;
(2)設![]() ,
,![]() 為數列
為數列![]() 的前
的前![]() 項和,求證:
項和,求證:![]() ;
;
(3)設![]() (
(![]() 為非零整數,
為非零整數,![]() ),試確定
),試確定![]() 的值,使得對任意
的值,使得對任意![]() ,都有
,都有![]() 成立.
成立.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【選修4-4:坐標系與參數方程】
在平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為:
的參數方程為: ![]() (
(![]() 為參數,
為參數, ![]() ),將曲線
),將曲線![]() 經過伸縮變換:
經過伸縮變換:  得到曲線
得到曲線![]() .
.
(1)以原點為極點, ![]() 軸的正半軸為極軸建立坐標系,求
軸的正半軸為極軸建立坐標系,求![]() 的極坐標方程;
的極坐標方程;
(2)若直線![]() (
(![]() 為參數)與
為參數)與![]() 相交于
相交于![]() 兩點,且
兩點,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】正三棱柱![]() (底面是正三角形,側棱垂直底面)的各條棱長均相等,
(底面是正三角形,側棱垂直底面)的各條棱長均相等,![]() 為
為![]() 的中點.
的中點.![]() 、
、![]() 分別是
分別是![]() 、
、![]() 上的動點(含端點),且滿足
上的動點(含端點),且滿足![]() .當
.當![]() 運動時,下列結論中正確的是______ (填上所有正確命題的序號).
運動時,下列結論中正確的是______ (填上所有正確命題的序號).

①平面![]() 平面
平面![]() ;
;
②三棱錐![]() 的體積為定值;
的體積為定值;
③![]() 可能為直角三角形;
可能為直角三角形;
④平面![]() 與平面
與平面![]() 所成的銳二面角范圍為
所成的銳二面角范圍為![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】學校某研究性學習小組在對學生上課注意力集中情況的調查研究中,發現其在40分鐘的一節課中,注意力指數![]() 與聽課時間
與聽課時間![]() (單位:分鐘)之間的關系滿足如圖所示的圖象,當
(單位:分鐘)之間的關系滿足如圖所示的圖象,當![]()
![]() 時,圖象是二次函數圖象的一部分,其中頂點
時,圖象是二次函數圖象的一部分,其中頂點![]() ,過點
,過點![]() ;當
;當![]()
![]() 時,圖象是線段BC,其中
時,圖象是線段BC,其中![]() .根據專家研究,當注意力指數大于62時,學習效果最佳.要使得學生學習效果最佳,則教師安排核心內容的時間段為____________.(寫成區間形式)
.根據專家研究,當注意力指數大于62時,學習效果最佳.要使得學生學習效果最佳,則教師安排核心內容的時間段為____________.(寫成區間形式)

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 的三邊長分別為
的三邊長分別為![]() ,
,![]() ,
,![]() ,M是AB邊上的點,P是平面ABC外一點.給出下列四個命題:①若
,M是AB邊上的點,P是平面ABC外一點.給出下列四個命題:①若![]() 平面ABC,則三棱錐
平面ABC,則三棱錐![]() 的四個面都是直角三角形;②若
的四個面都是直角三角形;②若![]() 平面ABC,且M是邊AB的中點,則有
平面ABC,且M是邊AB的中點,則有![]() ;③若
;③若![]() ,
,![]() 平面ABC,則
平面ABC,則![]() 面積的最小值為
面積的最小值為![]() ;④若
;④若![]() ,P在平面ABC上的射影是
,P在平面ABC上的射影是![]() 內切圓的圓心,則點P到平面ABC的距離為
內切圓的圓心,則點P到平面ABC的距離為![]() .其中正確命題的序號是________.(把你認為正確命題的序號都填上)
.其中正確命題的序號是________.(把你認為正確命題的序號都填上)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com