
已知函數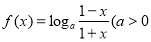 且
且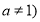 的圖象經過點
的圖象經過點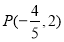 .
.
(1)求函數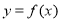 的解析式;
的解析式;
(2)設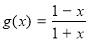 ,用函數單調性的定義證明:函數
,用函數單調性的定義證明:函數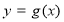 在區間
在區間 上單調遞減;
上單調遞減;
(3)解不等式: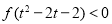 .
.
(1)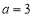 ,(2)詳見解析,(3)
,(2)詳見解析,(3)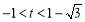 或
或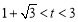 .
.
【解析】
試題分析:(1)求函數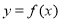 的解析式,只需確定
的解析式,只需確定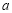 的值即可,由函數
的值即可,由函數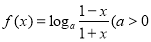 且
且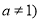 的圖象經過點
的圖象經過點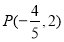 ,得
,得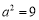 ,再由
,再由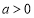 得
得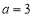 ,(2)用函數單調性的定義證明單調性,一設
,(2)用函數單調性的定義證明單調性,一設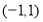 上的任意兩個值,二作差,三因式分解確定符號,(3)解不等式,一可代入解析式,轉化為解對數不等式,需注意不等號方向及真數大于零隱含條件,二利用函數單調性,去“
上的任意兩個值,二作差,三因式分解確定符號,(3)解不等式,一可代入解析式,轉化為解對數不等式,需注意不等號方向及真數大于零隱含條件,二利用函數單調性,去“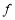 ”,注意定義域.
”,注意定義域.
試題解析:(1) ,解得:
,解得: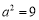 ∵
∵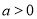 且
且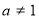 ∴
∴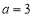 ; 3分
; 3分
(2)設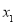 、
、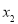 為
為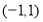 上的任意兩個值,且
上的任意兩個值,且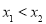 ,則
,則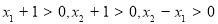
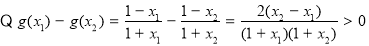 6分
6分
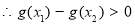 ,
,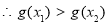
 在區間
在區間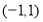 上單調遞減. 8分
上單調遞減. 8分
(3)方法(一):
由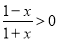 ,解得:
,解得: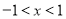 ,即函數
,即函數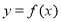 的定義域為
的定義域為 ; 10分
; 10分
先研究函數 在
在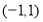 上的單調性.
上的單調性.
可運用函數單調性的定義證明函數 在區間
在區間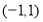 上單調遞減,證明過程略.
上單調遞減,證明過程略.
或設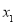 、
、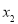 為
為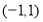 上的任意兩個值,且
上的任意兩個值,且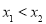 ,
,
由(2)得: 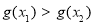
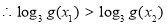 ,即
,即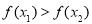
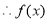 在區間
在區間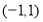 上單調遞減. 12分
上單調遞減. 12分
再利用函數 的單調性解不等式:
的單調性解不等式:
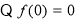 且
且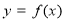 在
在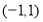 上為單調減函數.
上為單調減函數.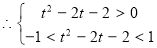 , 13分
, 13分
即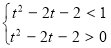 ,解得:
,解得:
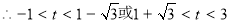 . 15分
. 15分
方法(二): 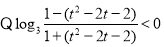
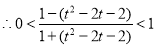 10分
10分
由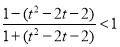 得:
得: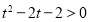 或
或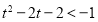 ;由
;由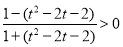 得:
得: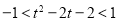 ,
,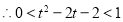 13分
13分
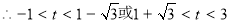 . 15分
. 15分
考點:函數解析式,函數單調性定義,解不等式.


湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com