
 已知PA⊥矩形ABCD所在平面,PA=AD,M、N分別是AB、PC的中點.
已知PA⊥矩形ABCD所在平面,PA=AD,M、N分別是AB、PC的中點.| ∥ |
. |
| 1 |
| 2 |
| ∥ |
. |
| 1 |
| 2 |
| ∥ |
. |
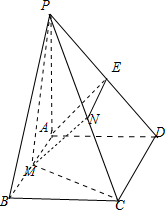


科目:高中數學 來源:2014屆安徽省高一下學期期中考試數學試卷(解析版) 題型:解答題
如圖,已知矩形ABCD所在平面外一點P,PA⊥平面ABCD,E、F分別是AB、
PC的中點.
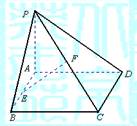
(1)求證:EF∥平面PAD;
(2)求證:EF⊥CD;
(3)若ÐPDA=45°求EF與平面ABCD所成的角的大小.
【解析】本試題主要考查了線面平行和線線垂直的運用,以及線面角的求解的綜合運用
第一問中,利用連AC,設AC中點為O,連OF、OE在△PAC中,∵ F、O分別為PC、AC的中點 ∴ FO∥PA …………①在△ABC中,∵ E、O分別為AB、AC的中點 ∴ EO∥BC ,又 ∵ BC∥AD ∴ EO∥AD …………②綜合①、②可知:平面EFO∥平面PAD∵ EF Ì 平面EFO ∴ EF∥平面PAD.
第二問中在矩形ABCD中,∵ EO∥BC,BC⊥CD ∴ EO⊥CD 又 ∵ FO∥PA,PA⊥平面AC ∴ FO⊥平面AC∴ EO為EF在平面AC內的射影 ∴ CD⊥EF.
第三問中,若ÐPDA=45°,則 PA=AD=BC ∵
EO
 BC,FO
BC,FO
 PA
PA
∴ FO=EO 又∵ FO⊥平面AC∴ △FOE是直角三角形 ∴ ÐFEO=45°
證:連AC,設AC中點為O,連OF、OE(1)在△PAC中,∵ F、O分別為PC、AC的中點∴ FO∥PA …………① 在△ABC中,∵ E、O分別為AB、AC的中點 ∴ EO∥BC ,又 ∵ BC∥AD ∴ EO∥AD …………②綜合①、②可知:平面EFO∥平面PAD
∵ EF Ì 平面EFO ∴ EF∥平面PAD.
(2)在矩形ABCD中,∵ EO∥BC,BC⊥CD∴ EO⊥CD 又 ∵ FO∥PA,PA⊥平面AC ∴ FO⊥平面AC ∴ EO為EF在平面AC內的射影 ∴ CD⊥EF.
(3)若ÐPDA=45°,則 PA=AD=BC ∵ EO
 BC,FO
BC,FO
 PA
PA
∴ FO=EO 又 ∵ FO⊥平面AC ∴ △FOE是直角三角形 ∴ ÐFEO=45°

查看答案和解析>>
科目:高中數學 來源: 題型:
己知在銳角ΔABC中,角![]() 所對的邊分別為
所對的邊分別為![]() ,且
,且![]()
(I )求角![]() 大小;
大小;
(II)當![]() 時,求
時,求![]() 的取值范圍.
的取值范圍.

20.如圖1,在平面內,![]() 是
是![]() 的矩形,
的矩形,![]() 是正三角形,將
是正三角形,將![]() 沿
沿![]() 折起,使
折起,使![]() 如圖2,
如圖2,![]() 為
為![]() 的中點,設直線
的中點,設直線![]() 過點
過點![]() 且垂直于矩形
且垂直于矩形![]() 所在平面,點
所在平面,點![]() 是直線
是直線![]() 上的一個動點,且與點
上的一個動點,且與點![]() 位于平面
位于平面![]() 的同側。
的同側。
(1)求證:![]() 平面
平面![]() ;
;
(2)設二面角![]() 的平面角為
的平面角為![]() ,若
,若![]() ,求線段
,求線段![]() 長的取值范圍。
長的取值范圍。


21.已知A,B是橢圓![]() 的左,右頂點,
的左,右頂點,![]() ,過橢圓C的右焦點F的直線交橢圓于點M,N,交直線
,過橢圓C的右焦點F的直線交橢圓于點M,N,交直線![]() 于點P,且直線PA,PF,PB的斜率成等差數列,R和Q是橢圓上的兩動點,R和Q的橫坐標之和為2,RQ的中垂線交X軸于T點
于點P,且直線PA,PF,PB的斜率成等差數列,R和Q是橢圓上的兩動點,R和Q的橫坐標之和為2,RQ的中垂線交X軸于T點
(1)求橢圓C的方程;
 (2)求三角形MNT的面積的最大值
(2)求三角形MNT的面積的最大值
22. 已知函數![]()
![]() ,
,
(Ⅰ)若![]() 在
在![]() 上存在最大值與最小值,且其最大值與最小值的和為
上存在最大值與最小值,且其最大值與最小值的和為![]() ,試求
,試求![]() 和
和![]() 的值。
的值。
(Ⅱ)若![]() 為奇函數:
為奇函數:
(1)是否存在實數![]() ,使得
,使得![]() 在
在![]() 為增函數,
為增函數,![]() 為減函數,若存在,求出
為減函數,若存在,求出![]() 的值,若不存在,請說明理由;
的值,若不存在,請說明理由;
(2)如果當![]() 時,都有
時,都有![]() 恒成立,試求
恒成立,試求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com