
���}Ŀ����֪����(sh��)![]()
![]() .
.
��1����![]() ����
����![]() ���{(di��o)�^(q��)�g��
���{(di��o)�^(q��)�g��
��2��ӑՓ![]() �����c����(sh��).
�����c����(sh��).
���𰸡���1��![]() ��
��![]() ���{(di��o)�f�p����
���{(di��o)�f�p����![]() ���{(di��o)�f��.��2����(d��ng)
���{(di��o)�f��.��2����(d��ng)![]() �r��
�r��![]() ��
��![]() �����c����(d��ng)
�����c����(d��ng)![]() �r��
�r��![]() ��
��![]() �����c.
�����c.
��������
��1����(d��o)�����![]() ��
��![]() �Ľ⼯�ɵý⣻
�Ľ⼯�ɵý⣻
��2����(d��ng)![]() �r���ɣ�1����õĆ��{(di��o)�Լ��ɵý⣻��(d��ng)
�r���ɣ�1����õĆ��{(di��o)�Լ��ɵý⣻��(d��ng)![]() �r���������(sh��)��(d��o)��(sh��)���O(sh��)��(d��o)����(sh��)�����c��
�r���������(sh��)��(d��o)��(sh��)���O(sh��)��(d��o)����(sh��)�����c��![]() �����
�����![]() ����Сֵ
����Сֵ![]() ������
������![]() ��
��![]() ���ɵý�.
���ɵý�.
��1����![]() �r��
�r��![]() ��
��![]() �Ķ��x���
�Ķ��x���![]() ��
��
![]() ��
��
��(d��ng)![]() �r��
�r��![]() ����(d��ng)
����(d��ng)![]() �r��
�r��![]() ��
��
����![]() ��
��![]() ���{(di��o)�f�p����
���{(di��o)�f�p����![]() ���{(di��o)�f��.
���{(di��o)�f��.
��2����(d��ng)![]() �r��
�r��![]() ��
��
![]()
![]() ����
����![]() ��
��![]() ���{(di��o)�f�p����
���{(di��o)�f�p����![]() ���{(di��o)�f����
���{(di��o)�f����
![]()
![]() ��
��![]() �����c��
�����c��
��(d��ng)![]() �r��
�r��![]() ��
��
��![]() ��
��
���![]() ��
��![]() ��
��![]() �φ��{(di��o)�f��.
�φ��{(di��o)�f��.
��![]() ��
��![]() ��
��
���Դ��ڌ���(sh��)![]() ��ʹ��
��ʹ��![]() .
.
��![]() �ϣ�
�ϣ�![]() ��
��![]() �ǜp����(sh��)��
�ǜp����(sh��)��
��![]() �ϣ�
�ϣ�![]() ��
��![]() ��������(sh��)��
��������(sh��)��
����![]() ����Сֵ��
����Сֵ��![]() ��
��
����![]() �M��
�M��![]() ��
��
��![]() ��
��
����![]()
![]()
![]() ��
��
���![]() ��
��![]()
![]() ��
��
�����![]() ��
��![]()
����![]() ��
��![]() �����c.
�����c.
�C����������(d��ng)![]() �r��
�r��![]() ��
��![]() �����c��
�����c��
��(d��ng)![]() �r��
�r��![]() ��
��![]() �����c.
�����c.



| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M�n�����]�� | ��һ | ��һ���M�n�����]�� |
| �߶� | �߶����M�n�����]�� | ���� | �������M�n�����]�� |
| ���� | �������M�n�����]�� | ���� | �������M�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D���������F![]() �У�
��![]() ����
����![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �����c��
�����c��![]() ��
��![]() �ϵ��c.
�ϵ��c.
��1����![]() ƽ��
ƽ��![]() ���C����
���C����![]() ƽ��
ƽ��![]() .
.
��2��������![]() ������ֵ.
������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���Fُ�ѳɞ�r���̼Һ�;��dz���A��һ�Nʡ�X����У�����M��ʽ�������̼�ͬ�r�����҈Fُ�W(w��ng).�F(xi��n)ǡ�������Fُ�W(w��ng)վ��![]() ���_չ�ˈFُ�I(y��)��(w��)��
���_չ�ˈFُ�I(y��)��(w��)�� ![]() ��ij�{(di��o)�鹫˾���{(di��o)���@���҈Fُ�W(w��ng)վ�ڱ��е��_չ��r���ı����Ѽ����ˈFُ�W(w��ng)վ���̼����S�C�س�ȡ��50���M���{(di��o)�飬���������@���҈Fُ�W(w��ng)վ����r���D��ʾ.
��ij�{(di��o)�鹫˾���{(di��o)���@���҈Fُ�W(w��ng)վ�ڱ��е��_չ��r���ı����Ѽ����ˈFُ�W(w��ng)վ���̼����S�C�س�ȡ��50���M���{(di��o)�飬���������@���҈Fُ�W(w��ng)վ����r���D��ʾ.
��1�������{(di��o)���50���̼������x�ɼң�����������Fُ�W(w��ng)վ�Ĕ�(sh��)������ȵĸ��ʣ�
��2�������{(di��o)���50���̼�����ȡ�ɼң���![]() ��ʾ�@�ɼ��̼҅��ӵĈFُ�W(w��ng)վ��(sh��)��֮��Ľ^��ֵ�����S�C׃��
��ʾ�@�ɼ��̼҅��ӵĈFُ�W(w��ng)վ��(sh��)��֮��Ľ^��ֵ�����S�C׃��![]() �ķֲ��к͔�(sh��)�W(xu��)������
�ķֲ��к͔�(sh��)�W(xu��)������
��3�����l��ҕ����ʣ��F(xi��n)��![]() ���S�C��ȡ3���Ѽ���Fُ�W(w��ng)վ���̼ң�ӛ����ǡ�ü����˃ɂ��Fُ�W(w��ng)վ���̼Ҕ�(sh��)��
���S�C��ȡ3���Ѽ���Fُ�W(w��ng)վ���̼ң�ӛ����ǡ�ü����˃ɂ��Fُ�W(w��ng)վ���̼Ҕ�(sh��)��![]() ��ԇ���¼���
��ԇ���¼���![]() ���ĸ���.
���ĸ���.

�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ��һ���΅^(q��)�Ѓɂ��½��Ŀ![]() ��
��![]() .
.![]() �Ŀ��һ��Ͷ�Y�~
�Ŀ��һ��Ͷ�Y�~![]() �c����
�c����![]() ���ƝM��
���ƝM��![]() .
.![]() �Ŀ��һ��Ͷ�Y�~
�Ŀ��һ��Ͷ�Y�~![]() �c����
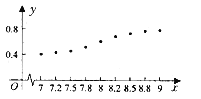
�c����![]() ���P(gu��n)ϵ��ɢ�c�D��ʾ������
���P(gu��n)ϵ��ɢ�c�D��ʾ������![]()
![]() ��
��![]() ��
��![]() .һ�̼������@�ɂ��Ŀһ���S�CͶ�Y������Ͷ�Y
.һ�̼������@�ɂ��Ŀһ���S�CͶ�Y������Ͷ�Y![]() �Ŀ�����^10�����}δע�����~��λ�ģ���λ������fԪ��.Ͷ�Y
�Ŀ�����^10�����}δע�����~��λ�ģ���λ������fԪ��.Ͷ�Y![]() ��
��![]() �����.
�����.
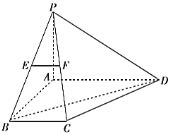
��1������С���˷���![]() �c
�c![]() �Ļؚwֱ�����̣�
�Ļؚwֱ�����̣�
��2���̼�Ͷ�Y![]() �Ŀ�ĸ�����0.4��Ͷ�Y
�Ŀ�ĸ�����0.4��Ͷ�Y![]() �Ŀ�ĸ�����0.6.�O(sh��)�̼��@��Ͷ�Y�@�õ��������ֵ��
�Ŀ�ĸ�����0.6.�O(sh��)�̼��@��Ͷ�Y�@�õ��������ֵ��![]() �����ã�1���ĽY(ji��)������
�����ã�1���ĽY(ji��)������![]() .
.
��������ʽ��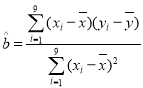 ��
��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ��ij��I(y��)푑�(y��ng)ʡ����̖�٣����F(xi��n)���O(sh��)���M�и��죬���˷����O(sh��)�����ǰ���Ч�����F(xi��n)���O(sh��)�����ǰ�����a(ch��n)�Ĵ����a(ch��n)Ʒ�и���ȡ��![]() ���a(ch��n)Ʒ����ӱ����z�yһ��|(zh��)��ָ��(bi��o)ֵ����ԓ��|(zh��)��ָ��(bi��o)ֵ����
���a(ch��n)Ʒ����ӱ����z�yһ��|(zh��)��ָ��(bi��o)ֵ����ԓ��|(zh��)��ָ��(bi��o)ֵ����![]() ��(n��i)�Įa(ch��n)Ʒҕ��ϸ�Ʒ����t�鲻�ϸ�Ʒ.��D���O(sh��)�����ǰ�Ęӱ����l�ʷֲ�ֱ���D����
��(n��i)�Įa(ch��n)Ʒҕ��ϸ�Ʒ����t�鲻�ϸ�Ʒ.��D���O(sh��)�����ǰ�Ęӱ����l�ʷֲ�ֱ���D����![]() ���O(sh��)������Ęӱ����l��(sh��)�ֲ���.
���O(sh��)������Ęӱ����l��(sh��)�ֲ���.
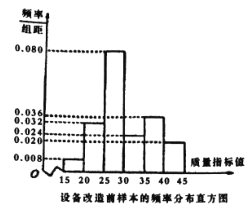
�����O(sh��)������ӱ����l��(sh��)�ֲ���
�|(zh��)��ָ��(bi��o)ֵ |
|
|
|
|
|
|
�l��(sh��) |
|
|
|
|
|
|
��1����������![]() ��(li��n)�������Д��Ƿ���
��(li��n)�������Д��Ƿ���![]() �İ����J(r��n)��ԓ��I(y��)���a(ch��n)���@�N�a(ch��n)Ʒ���|(zh��)��ָ��(bi��o)ֵ�c�O(sh��)��������P(gu��n)��
�İ����J(r��n)��ԓ��I(y��)���a(ch��n)���@�N�a(ch��n)Ʒ���|(zh��)��ָ��(bi��o)ֵ�c�O(sh��)��������P(gu��n)��
�O(sh��)�����ǰ | �O(sh��)������ | ��Ӌ | |
�ϸ�Ʒ | |||
���ϸ�Ʒ | |||
��Ӌ |
��2������(j��)�l�ʷֲ�ֱ���D�ͱ� �ṩ�Ĕ�(sh��)��(j��)��ԇ�Įa(ch��n)Ʒ�ϸ��ʵĽǶȌ�����ǰ���O(sh��)��ă�(y��u)���M�б��^��
��3����I(y��)�����ϸ�Ʒȫ���N������(j��)�͑����ϸ�Ʒ�M�е�ӛ��(x��)�֣��|(zh��)��ָ��(bi��o)ֵ����![]() ��(n��i)�Ķ���һ��Ʒ��ÿ���ۃr
��(n��i)�Ķ���һ��Ʒ��ÿ���ۃr![]() Ԫ���|(zh��)��ָ��(bi��o)ֵ����
Ԫ���|(zh��)��ָ��(bi��o)ֵ����![]() ��
��![]() ��(n��i)�Ķ������Ʒ��ÿ���ۃr
��(n��i)�Ķ������Ʒ��ÿ���ۃr![]() Ԫ�������ĺϸ�Ʒ��������Ʒ��ÿ���ۃr
Ԫ�������ĺϸ�Ʒ��������Ʒ��ÿ���ۃr![]() Ԫ.����(j��)��
Ԫ.����(j��)��![]() �Ĕ�(sh��)��(j��)����ԓ�M�ӱ���һ��Ʒ������Ʒ������Ʒ�����ںϸ�Ʒ�е��l�ʴ�������Юa(ch��n)Ʒ�г鵽һ������(y��ng)�ȼ��a(ch��n)Ʒ�ĸ���.�F(xi��n)��һ����S�Cُ�I�ɼ��a(ch��n)Ʒ���O(sh��)��֧�����M�Þ�
�Ĕ�(sh��)��(j��)����ԓ�M�ӱ���һ��Ʒ������Ʒ������Ʒ�����ںϸ�Ʒ�е��l�ʴ�������Юa(ch��n)Ʒ�г鵽һ������(y��ng)�ȼ��a(ch��n)Ʒ�ĸ���.�F(xi��n)��һ����S�Cُ�I�ɼ��a(ch��n)Ʒ���O(sh��)��֧�����M�Þ�![]() ����λ��Ԫ������
����λ��Ԫ������![]() �ķֲ��к͔�(sh��)�W(xu��)����.
�ķֲ��к͔�(sh��)�W(xu��)����.
����
|
|
|
|
|
|
|
|
|
|
|
|
![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����С�}�M��13�֣�
�����ˆT���M����վ���ij헾��и�ݗ��Σ�U���΄�(w��)��ÿ��ֻ��һ�����Mȥ����ÿ����ֻ��һ�Σ������r�g�����^10��犣������һ����10��犃�(n��i)��������΄�(w��)�t������������һ���ˣ��F(xi��n)��һ��ֻ�мס��ҡ��������˿��ɣ���������������΄�(w��)�ĸ��ʷքe![]()
![]() �����O(sh��)
�����O(sh��)![]() ������ȣ��Ҽٶ������ܷ�����΄�(w��)���¼������.
������ȣ��Ҽٶ������ܷ�����΄�(w��)���¼������.
��1������������ȣ��Ҵ�֮��������������ˣ����΄�(w��)�ܱ���ɵĸ��ʣ�����׃?n��i)����˱��ɳ����Ⱥ�����΄�(w��)�ܱ���ɵĸ����Ƿ�l(f��)��׃����
��2������ijָ��������ˣ��@�����˸���������΄�(w��)�ĸ������Ξ�![]() ������
������![]() ��
��![]() ��һ�����У��������ɳ��ˆT��(sh��)Ŀ
��һ�����У��������ɳ��ˆT��(sh��)Ŀ![]() �ķֲ��к;�ֵ����(sh��)��������
�ķֲ��к;�ֵ����(sh��)��������![]() ��
��
��3���ٶ�![]() ��ԇ���������ӵ��Ⱥ�����ɳ��ˆT����ʹ�����ɳ����ˆT��(sh��)Ŀ�ľ�ֵ����(sh��)���������_����С��
��ԇ���������ӵ��Ⱥ�����ɳ��ˆT����ʹ�����ɳ����ˆT��(sh��)Ŀ�ľ�ֵ����(sh��)���������_����С��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ��ÿ��9�µ������LJ��ҾW(w��ng)�j(lu��)��ȫ������.ij�W(xu��)У���{(di��o)�鱾У�W(xu��)�����W(w��ng)�j(lu��)��ȫ֪�R���˽���r���M���ˡ��W(w��ng)�j(lu��)��Ϣ�����yԇ����ӣ����S�C��ȡ50�˵Ĝyԇ�ɿ��L�����l�ʷֲ�ֱ���D��D��ʾ:

��1��ij�W(xu��)���Ĝyԇ�ɿ���75�֣����X��ԓͬ�W(xu��)�Ĝyԇ�ɿ��Ͳ���?�f�����ɣ�
��2�����ɿ���![]() ��(n��i)���x�����ϸ������ɿ���
��(n��i)���x�����ϸ������ɿ���![]() ��(n��i)���x�������ϸ���.��Ո�������
��(n��i)���x�������ϸ���.��Ո�������![]() ��(li��n)���a�������� ���Ƿ���90%�İ��J(r��n)��W(w��ng)�j(lu��)��ȫ֪�R��������r�c�Ԅe���P(gu��n)?�f��������ɣ�
��(li��n)���a�������� ���Ƿ���90%�İ��J(r��n)��W(w��ng)�j(lu��)��ȫ֪�R��������r�c�Ԅe���P(gu��n)?�f��������ɣ�
�ϸ� | ���ϸ� | ��Ӌ | |
���� | 26 | ||
�� | 6 | ||
��Ӌ |
��3���ڣ�2����ǰ���£���50�˰��Ƿ�ϸ����÷ӳ�ӵķ�����ȡ5�ˣ��ُ�5�����S�C��ȡ2�ˣ���ǡ��2�˶��ϸ�ĸ���.��:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.65 | 10.828 |
![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ�������{(di��o)�顰�p11�����M�����r��ijУ�y(t��ng)ӋС�M�քe���L��![]() ��
��![]() �ɂ�С�^(q��)��20����ͥ��������(d��ng)�յ����M�~��
�ɂ�С�^(q��)��20����ͥ��������(d��ng)�յ����M�~��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �ֽM���քe���l�ʷֲ�ֱ���D�c�o�~�D�y(t��ng)Ӌ���£���λ��Ԫ����
�ֽM���քe���l�ʷֲ�ֱ���D�c�o�~�D�y(t��ng)Ӌ���£���λ��Ԫ����
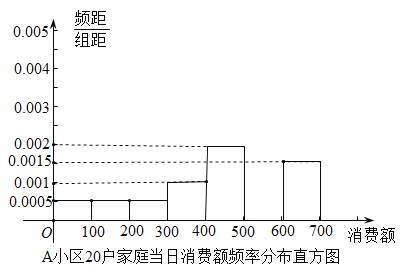
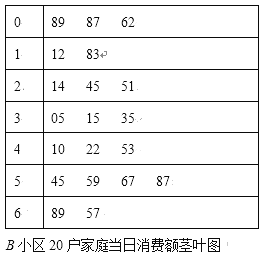
��1���քeӋ��ɂ�С�^(q��)�@20����ͥ��(d��ng)�����M�~��![]() ���l�ʣ����aȫ�l�ʷֲ�ֱ���D��
���l�ʣ����aȫ�l�ʷֲ�ֱ���D��
��2���քe�ăɂ�С�^(q��)�S�C�xȡ1����ͥ�����@�ɑ���ͥ��(d��ng)�����M�~��![]() �đ���(sh��)��1�r�ĸ��ʣ��l�ʮ�(d��ng)������ʹ�ã���
�đ���(sh��)��1�r�ĸ��ʣ��l�ʮ�(d��ng)������ʹ�ã���
��3���\�����W(xu��)�y(t��ng)Ӌ֪�R�������^�ɂ�С�^(q��)�Į�(d��ng)�վW(w��ng)ُ���Mˮƽ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ��ֱ��![]() �c���タ
�c���タ![]()
![]() �ཻ��
�ཻ��![]() ��
��![]() ���c����
���c����![]() ����
����![]() ��
��![]() ��
��![]() �S���x�ij˷e��
�S���x�ij˷e��![]() ��
��
��1����![]() �ķ��̣�
�ķ��̣�
��2���O(sh��)�c![]() �钁�タ
�钁�タ![]() �Ľ��c����(d��ng)
�Ľ��c����(d��ng)![]() ��e��С�r����ֱ��
��e��С�r����ֱ��![]() �ķ��̣�
�ķ��̣�
�鿴�𰸺ͽ���>>
�ٶ����� - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��ƽ�_ | �W(w��ng)���к���Ϣ�e�^(q��) | ����p�_�e�^(q��) | ��vʷ̓�o���x�к���Ϣ�e�^(q��) | �����֙�(qu��n)�e�^(q��)
�`���Ͳ�����Ϣ�e���Ԓ��027-86699610 �e���]�䣺58377363@163.com