
【題目】已知函數f(x)=logm![]() (m>0且m≠1),
(m>0且m≠1),
(I)判斷f(x)的奇偶性并證明;
(II)若m=![]() ,判斷f(x)在(3,+∞)的單調性(不用證明);
,判斷f(x)在(3,+∞)的單調性(不用證明);
(III)若0<m<1,是否存在β>α>0,使f(x)在[α,β]的值域為[logmm(β-1),logm(α-1)]?若存在,求出此時m的取值范圍;若不存在,請說明理由.
【答案】(Ⅰ)f(x)是奇函數(Ⅱ)見解析(Ⅲ)![]() .
.
【解析】
(Ⅰ)先求定義域,再判斷![]() 與f(x)關系,最后根據奇偶性定義作判斷與證明,(Ⅱ)根據單調性定義進行判斷,(Ⅲ)先根據單調性確定方程組,轉化為一元二次方程有兩正根,再根據二次方程實根分布列方程,最后解不等式組得結果.
與f(x)關系,最后根據奇偶性定義作判斷與證明,(Ⅱ)根據單調性定義進行判斷,(Ⅲ)先根據單調性確定方程組,轉化為一元二次方程有兩正根,再根據二次方程實根分布列方程,最后解不等式組得結果.
解:(Ⅰ)f(x)是奇函數;證明如下:
由![]() 解得x<-3或x>3,
解得x<-3或x>3,
所以f(x)的定義域為(-∞,-3)∪(3,+∞),關于原點對稱.
∵![]() =
=![]() ,
,
故f(x)為奇函數/
(Ⅱ)任取x1,x2∈(3,+∞)且x1<x2,
![]() =
=![]() ,
,
∵(x1-3)(x2+3)-(x1+3)(x2-3)<0,∴(x1-3)(x2+3)<(x1+3)(x2-3),
即![]() ,
,
當m=![]() 時,
時,![]() ,即f(x1)<f(x2).
,即f(x1)<f(x2).
故f(x)在(3,+∞)上單調遞減.
(Ⅲ)由(Ⅱ)知,當0<m<1時,f(x)在[α,β]上單調遞減.
假設存在β>α>0,使f(x)在[α,β]的值域為[logmm(β-1),logm(α-1)].
則有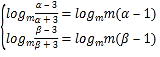 ,∴
,∴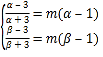 .
.
所以α,β是方程![]() 的兩正根,
的兩正根,
整理得mx2+(2m-1)x-3m+3=0在(0,+∞)有2個不等根α和β.
令h(x)=mx2+(2m-1)x-3m+3,則h(x)在(0,+∞)有2個零點,
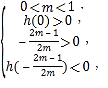 解得
解得![]() ,
,
故m的取值范圍為![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】某校舉行漢字聽寫比賽,為了了解本次比賽成績情況,從得分不低于50分的試卷中隨機抽取100名學生的成績(得分均為整數,滿分100分)進行統計,請根據頻率分布表中所提供的數據,解答下列問題:
組號 | 分組 | 頻數 | 頻率 |
第1組 | [50,60) | 5 | 0.05 |
第2組 | [60,70) |
| 0.35 |
第3組 | [70,80) | 30 |
|
第4組 | [80,90) | 20 | 0.20 |
第5組 | [90,100] | 10 | 0.10 |
合計 | 100 | 1.00 |
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)若從成績較好的第3、4、5組中按分層抽樣的方法抽取6人參加市漢字聽寫比賽,并從中選出2人做種子選手,求2人中至少有1人是第4組的概率。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓C:![]() ,直線L:
,直線L:![]() .
.
⑴ 求證:對![]() ,直線L與圓C總有兩個交點;
,直線L與圓C總有兩個交點;
⑵ 求直線L與圓C截得的線段的最短長度,以及此時直線L的方程;;
⑶ 設直線L與圓C交于A、B兩點若︱AB︱=![]() ,求L的傾斜角.
,求L的傾斜角.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】記函數![]() 的定義域為D,若存在
的定義域為D,若存在![]() ,使
,使![]() 成立,則稱以
成立,則稱以![]() 為坐標的點是函數
為坐標的點是函數![]() 的圖象上的“穩定點”.
的圖象上的“穩定點”.
(1)若函數![]() 的圖象上有且只有兩個相異的“穩定點”,試求實數a的取值范圍;
的圖象上有且只有兩個相異的“穩定點”,試求實數a的取值范圍;
(2)已知定義在實數集R上的奇函數![]() 存在有限個“穩定點”,求證:
存在有限個“穩定點”,求證:![]() 必有奇數個“穩定點”.
必有奇數個“穩定點”.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】正方體![]() 的棱長為1,線段
的棱長為1,線段![]() 上有兩個動點
上有兩個動點![]() , 且
, 且![]() , 則下列結論中錯誤的是( )
, 則下列結論中錯誤的是( )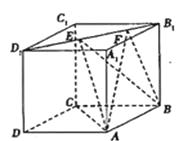
A.![]()
B.三棱錐![]() 的體積為定值
的體積為定值
C.二面角![]() 的大小為定值
的大小為定值
D.異面直線![]() 所成角為定值
所成角為定值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解少年兒童的肥胖是否與常喝碳酸飲料有關,現對30名六年級學生進行了問卷調查,得到數據如表所示(平均每天喝500ml以上為常喝,體重超過50kg為肥胖):
常喝 | 不常喝 | 合計 | |
肥胖 | 2 | 8 | |
不肥胖 | 18 | ||
合計 | 30 |
(Ⅰ)請將上面的列聯表補充完整;
(Ⅱ)是否有99%的把握認為肥胖與常喝碳酸飲料有關?說明你的理由.
| 0.050 0.010 |
| 3.841 6.635 |
參考數據:
附:![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一圓臺上底半徑為5cm,下底半徑為10cm,母線AB長為20cm,其中A在上底面上,B在下底面上,從AB中點M,拉一條繩子,繞圓臺的側面一周轉到B點,則這條繩子最短長為 cm.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(2015·上海)如圖,圓錐的頂點為P,底面的一條直徑為AB,C為半圓弧AB的中點,E為劣弧CB的中點. 已知PO=2,OA=1,求三棱錐P-AOC的體積,并求異面直線PA與OE所成角的大小.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com