
【題目】①在同一坐標(biāo)系中,![]() 與
與![]() 的圖象關(guān)于
的圖象關(guān)于![]() 軸對稱;
軸對稱;
②![]() 是奇函數(shù);
是奇函數(shù);
③![]() 的圖象關(guān)于
的圖象關(guān)于![]() 成中心對稱;
成中心對稱;
④![]() 的最大值為
的最大值為![]() ;
;
⑤![]() 的單調(diào)增區(qū)間:
的單調(diào)增區(qū)間:![]() 。
。
以上五個(gè)判斷正確有____________________(寫上所有正確判斷的序號)。
【答案】![]()
【解析】
結(jié)合相關(guān)知識對給出的每個(gè)選項(xiàng)分別進(jìn)行分析、判斷可得正確的結(jié)論.
對于①,由于![]() ,則在同一坐標(biāo)系中,
,則在同一坐標(biāo)系中,![]() 與
與![]()
的圖象關(guān)于![]() 軸對稱,故①正確;
軸對稱,故①正確;
對于② ,函數(shù)![]() 的定義域?yàn)?/span>
的定義域?yàn)?/span>![]() ,又
,又![]() ,所以函數(shù)是奇函數(shù),故②正確;
,所以函數(shù)是奇函數(shù),故②正確;
對于③,因?yàn)?/span>![]() 的對稱中心
的對稱中心![]() ,將函數(shù)
,將函數(shù)![]() 的圖象向左平移2單位,再向上平移1單位,可得到
的圖象向左平移2單位,再向上平移1單位,可得到![]() 的圖象的對稱中心為
的圖象的對稱中心為![]() ,所以③正確;
,所以③正確;
對于④,![]() ,因?yàn)?/span>
,因?yàn)?/span>![]() ,所以
,所以![]() ,所以當(dāng)x=0時(shí)函數(shù)取得的最小值為
,所以當(dāng)x=0時(shí)函數(shù)取得的最小值為![]() ,故④不正確;
,故④不正確;
⑤ 函數(shù)![]() 的單調(diào)增區(qū)間為
的單調(diào)增區(qū)間為![]() ,故⑤不正確.
,故⑤不正確.
綜上可得①②③正確.
故答案為:①②③.


 閱讀快車系列答案
閱讀快車系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某機(jī)構(gòu)在某一學(xué)校隨機(jī)抽取30名學(xué)生參加環(huán)保知識測試,測試成績(單位:分)如圖所示,假設(shè)得分值的中位數(shù)為me , 眾數(shù)為m0 , 平均值為 ![]() ,則( )
,則( ) 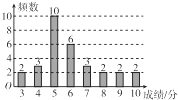
A.me=m0= ![]()
B.me=m0< ![]()
C.me<m0< ![]()
D.m0<me< ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知f(x)= ![]() ,g(x)=ax3﹣x2﹣x+b(a,b∈R,a≠0),g(x)的圖象C在x=﹣
,g(x)=ax3﹣x2﹣x+b(a,b∈R,a≠0),g(x)的圖象C在x=﹣ ![]() 處的切線方程是y=
處的切線方程是y= ![]() .
.
(1)若求a,b的值,并證明:當(dāng)x∈(﹣∞,2]時(shí),g(x)的圖象C上任意一點(diǎn)都在切線y= ![]() 上或在其下方;
上或在其下方;
(2)求證:當(dāng)x∈(﹣∞,2]時(shí),f(x)≥g(x).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】函數(shù)y=f(x)在![]() 上是增函數(shù),函數(shù)y=f(x+2)是偶函數(shù),則( )
上是增函數(shù),函數(shù)y=f(x+2)是偶函數(shù),則( )
A. f(1)<f(2.5)<f(3.5) B. f(3.5)<f(1)<f(2.5)
C. f(3.5)<f(2.5)<f(1) D. f(2.5)<f(1)<f(3.5)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】銳角△ABC中,角A,B,C所對的邊分別為a,b,c,且acosB+bcosA= ![]() csinC.
csinC.
(1)求cosC;
(2)若a=6,b=8,求邊c的長.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知正項(xiàng)等比數(shù)列{an}滿足a7=a6+2a5 , 若存在兩項(xiàng)am , an使得 ![]() ,則
,則 ![]() 的最小值為( )
的最小值為( )
A.![]()
B.![]()
C.![]()
D.不存在
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】袋中裝有紅球3個(gè)、白球2個(gè)、黑球1個(gè),從中任取2個(gè),則互斥而不對立的兩個(gè)事件是( )
A. 至少有一個(gè)白球;至少有一個(gè)紅球 B. 至少有一個(gè)白球;紅、黑球各一個(gè)
C. 恰有一個(gè)白球;一個(gè)白球一個(gè)黑球 D. 至少有一個(gè)白球;都是白球
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在一個(gè)半徑為1的半球材料中截取兩個(gè)高度均為![]() 的圓柱,其軸截面如圖所示.設(shè)兩個(gè)圓柱體積之和為
的圓柱,其軸截面如圖所示.設(shè)兩個(gè)圓柱體積之和為![]() .
.

(1)求![]() 的表達(dá)式,并寫出
的表達(dá)式,并寫出![]() 的取值范圍;
的取值范圍;
(2)求兩個(gè)圓柱體積之和![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com