
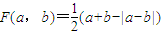 ,如果函數
,如果函數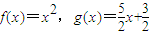 ,h(x)=-x+2,那么函數G(x)=F(F(f(x),g(x)),h(x))的最大值等于 .
,h(x)=-x+2,那么函數G(x)=F(F(f(x),g(x)),h(x))的最大值等于 .  天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
| 1 |
| 2 |
| 1 |
| 2+an |
| 4 |
| 5 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 |
| 2 |
| 1 |
| 2+an |
| 4 |
| 5 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 ,2an+1=f(an)+15,bn=
,2an+1=f(an)+15,bn=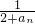 (n∈N*).
(n∈N*). )n]≤Sn<2.
)n]≤Sn<2.查看答案和解析>>
科目:高中數學 來源:2011年廣東省華南師大附中高三臨門一腳綜合測試數學試卷(理科)(解析版) 題型:解答題
 ,2an+1=f(an)+15,bn=
,2an+1=f(an)+15,bn=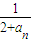 (n∈N*).已知不等式|f(x)≤2x2+4x-30|對任意實數x均成立.
(n∈N*).已知不等式|f(x)≤2x2+4x-30|對任意實數x均成立.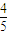 )n]≤Sn<2.
)n]≤Sn<2.查看答案和解析>>
科目:高中數學 來源:2009年上海市浦東新區建平中學高考數學三模試卷(理科)(解析版) 題型:解答題
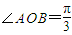 ,求曲線C的方程;
,求曲線C的方程;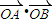 為定值T?指出T的值;
為定值T?指出T的值;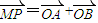 ,當a=-2,m變化時,求點P的軌跡方程;
,當a=-2,m變化時,求點P的軌跡方程;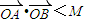 恒成立?如果存在,求出的M得最小值;如果不存在,說明理由.
恒成立?如果存在,求出的M得最小值;如果不存在,說明理由.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com