
 (a為實常數).
(a為實常數). .
.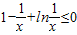 ≤0,即ln
≤0,即ln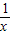
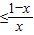 ,令x=
,令x= 適當變形即可證明.
適當變形即可證明. ,其定義域為(0,+∞),g′(x)=-2+
,其定義域為(0,+∞),g′(x)=-2+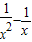 =
=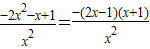 ,,
,,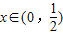 ; 令g′(x)<0,并結合定義域知
; 令g′(x)<0,并結合定義域知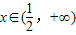 ;
; );單調減區間為
);單調減區間為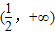 .
.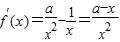 ,
, ,當x∈(0,1)時,f′(x)>0,f(x)單調遞增;
,當x∈(0,1)時,f′(x)>0,f(x)單調遞增;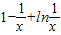 在x=1處取得最大值0.
在x=1處取得最大值0.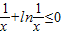 ,
,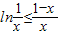 ,令x=
,令x=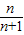 (0<x<1),則
(0<x<1),則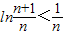 ,即ln(n+1)-lnn
,即ln(n+1)-lnn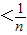 ,
,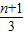 =ln(n+1)-ln3=[ln(n+1)-lnn]+[lnn-ln(n-1)]+…+(ln4-ln3)
=ln(n+1)-ln3=[ln(n+1)-lnn]+[lnn-ln(n-1)]+…+(ln4-ln3)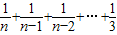 .
.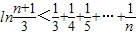 .
.

 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源:2012-2013學年浙江省溫州市蒼南中學高三(上)期中數學試卷(文科)(解析版) 題型:解答題
 (a為實常數).
(a為實常數). 上有解,求實數a的取值范圍;
上有解,求實數a的取值范圍; ,它的前n項和為Sn,求證:
,它的前n項和為Sn,求證: .
.查看答案和解析>>
科目:高中數學 來源:2012-2013學年浙江省溫州市蒼南中學高三(上)期中數學試卷(文科)(解析版) 題型:解答題
 (a為實常數).
(a為實常數). 上有解,求實數a的取值范圍;
上有解,求實數a的取值范圍; ,它的前n項和為Sn,求證:
,它的前n項和為Sn,求證: .
.查看答案和解析>>
科目:高中數學 來源:2011-2012學年江西省南昌三中高三(上)第三次月考數學試卷(理科)(解析版) 題型:解答題
 (a為實常數).
(a為實常數). .
.查看答案和解析>>
科目:高中數學 來源:2012-2013學年安徽省阜陽市潁上一中高考數學三模試卷(理科)(解析版) 題型:解答題
 (a為實常數).
(a為實常數). .
.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com