自拍视频在线观看,亚洲精选一区二区,成人1区

某農科所對冬季晝夜溫差大小與某反季節大豆新品種發芽多少之間的關系進行分析研究，他們分別記錄了12月1日至12月5日的每天晝夜溫差與實驗室每天每100棵種子中的發芽數，得到如下資料：

日期	12月1日	12月2日	12月3日	12月4日	12月5日
溫差x(℃)	10	11	13	12	8
發芽y(顆)	23	25	30	26	16

該農科所確定的研究方案是：先從這5組數據中選取3組數據求線性回歸方程，剩下的2組數據用于回歸方程檢驗．
回歸直線方程參考公式：

（1）請根據12月2日至12月4日的數據，求出y關于x的線性回歸方程

；
(2)若由線性回歸方程得到的估計數據與所選出的檢驗數據的誤差均不超過2顆，則
認為得到的線性回歸方程是可靠的，試問(1)中所得的線性回歸方程是否可靠？
（3）請預測溫差為14℃的發芽數。

(1)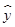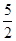＝x－3.(2)該研究所得到的線性回歸方程是可靠的．（3）32

解析試題分析：(1)由數據求得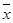，＝12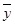，＝27，               2分
由公式求得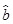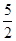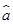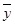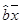．＝，＝－＝－3.            4分
所以y關于x的線性回歸方程為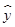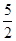＝x－3.           6分
(2)當x＝10時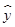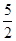，＝×10－3＝22，|22－23|<2；
當x＝8時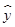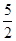，＝×8－3＝17，|17－16|<2.
所以該研究所得到的線性回歸方程是可靠的．        10分
（3）當x=14時，有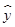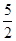＝x－3=35-3=32所以當溫差為14℃的發芽數約為32顆。 12分
考點：本題考查了線性回歸方程及運用
點評：本題中已知y對x呈線性相關關系，可直接根據給出數據求出b和a，得到回歸直線方程；而正確理解系數b的意義也是解題的關鍵

練習冊系列答案

年級	高中課程	年級	初中課程
高一	高一免費課程推薦！	初一	初一免費課程推薦！
高二	高二免費課程推薦！	初二	初二免費課程推薦！
高三	高三免費課程推薦！	初三	初三免費課程推薦！
更多初中、高中輔導課程推薦,點擊進入>>

相關習題

科目：高中數學 來源： 題型：解答題

以下莖葉圖記錄了甲、乙兩組各四名同學的植樹棵數．乙組記錄中有一個數據模糊，無法確認，在圖中以X表示．

(1)如果X＝8，求乙組同學植樹棵數的平均數和方差；
(2)如果X＝9，分別從甲、乙兩組中隨機選取一名同學，求這兩名同學的植樹總棵數為19的概率．
(注：方差s²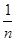＝[(x₁－)²＋(x₂－)²＋…＋(x_n－)²])，其中為x₁，x₂，…，x_n的平均數)

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

2012年元旦、春節前夕，各個物流公司都出現了爆倉現象，直接原因就是網上瘋狂的購物．某商家針對人們在網上購物的態度在某城市進行了一次調查，共調查了124人，其中女性70人，男性54人．女性中有43人對網上購物持贊成態度，另外27人持反對態度；男性中有21人贊成網上購物，另外33人持反對態度．
(Ⅰ) 估計該地區對網上購物持贊成態度的比例；
(Ⅱ) 有多大的把握認為該地區對網上購物持贊成態度與性別有關；
附：表1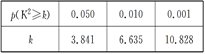

K²＝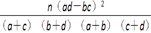

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

某校舉行運動會，組委會招墓了16名男志愿者和14名女志愿者，調查發現，男、女志愿者中分別有10人和6人喜愛運動，其余不喜愛。
（1）根據以上數據完成以下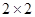列聯表：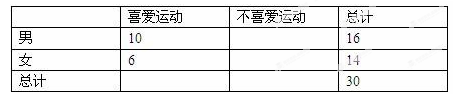

（2）根據列聯表的獨立性檢驗，有多大的把握認為性別與喜愛運動有關？
（3）從不喜愛運動的女志愿者中和喜愛運動的女志愿者中各選1人，求其中不喜愛運動的女生甲及喜愛運動的女生乙至少有一人被選取的概率。
參考公式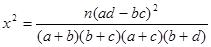：（其中）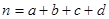


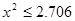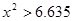是否有關聯	沒有關聯	90%	95%	99%

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

我校高三年級進行了一次水平測試.用系統抽樣的方法抽取了50名學生的數學成績,準備進行分析和研究.經統計成績的分組及各組的頻數如下:
[40,50), 2;   [50,60), 3; [60,70), 10; [70,80), 15;   [80,90), 12; [90,100], 8.
（Ⅰ）完成樣本的頻率分布表；畫出頻率分布直方圖.
（Ⅱ）估計成績在85分以下的學生比例；
（Ⅲ）請你根據以上信息去估計樣本的眾數、中位數、平均數.（精確到0.01）
頻率分布表                       頻率分布直方圖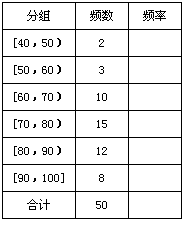

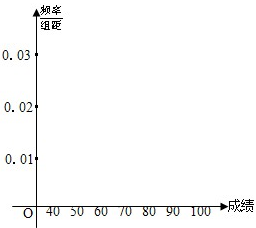
查看答案和解析>>

科目：高中數學 來源： 題型：解答題

在對人們的休閑方式的一次調查中，共調查了124人，其中女性70人，男性54人。女性中有43人主要的休閑方式是看電視，另外27人主要的休閑方式是運動；男性中有21人主要的休閑方式是看電視，另外33人主要的休閑方式是運動。
（1）根據以上數據建立一個的列聯表；
（2）判斷性別與休閑方式是否有關系。
（本題可以參考兩個分類變量x和y有關系的可信度表:）

P(k²>k)	0.50	0.40	0.25	0.15	0.10	0.05	0.025	0.010	0.005	0.001
k	0.455	0.708	1.323	2.072	2.706	3.841	5.024	6.635	7.879	10.83

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

某重點中學的高二英語老師Vivien，為調查學生的單詞記憶時間開展問卷調查。發現在回收上來的1000份有效問卷中，有600名同學們背英語單詞的時間安排在白天，另外400名學生晚上臨睡前背。Vivien老師用分層抽樣的方法抽取50名學生進行實驗，實驗方法是使兩組學生記憶40個無意義音節（如XIQ、GEH），均要求在剛能全部記清時就停止識記，并在8小時后進行記憶測驗。不同的是，甲組同學識記結束后一直不睡覺，8小時后測驗；乙組同學識記停止后立刻睡覺，8小時后叫醒測驗。
乙組同學識記停止8小時后的準確回憶（保持）情況如圖。

（1）由分層抽樣方法，抽取的50名學生乙組應有幾名？
（2）從乙組準確回憶音節數在[8,20)范圍內的學生中隨機選2人，求兩人均準確回憶12個（含12個）以上的概率；
（3）若從是否睡前記憶單詞和單詞小測能否優秀進行統計，運用2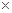2列聯表進行獨立性檢驗，經計算K²=4．069，參考下表你能得到什么統計學結論？

P(K

≥k₀)

0.100

0.050

0.025

0.010

0.001

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

某單位為了提高員工素質，舉辦了一場跳繩比賽，其中男員工12人，女員工18人，其成績編成如圖所示的莖葉圖（單位：分），分數在175分以上（含175分）者定為“運動健將”，并給予特別獎勵，其他人員則給予“運動積極分子”稱號.

（1）若用分層抽樣的方法從“運動健將”和“運動積極分子”中抽取10人，然后再從這10人中選4人，求至少有1人是“運動健將”的概率；
（2）若從所有“運動健將”中選3名代表，求所選代表中女“運動健將”恰有2人的概率.

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

（本小題滿分12分）
某大學高等數學老師上學期分別采用了兩種不同的教學方式對甲、乙兩個大一新生班進行教改試驗（兩個班人數均為60人，入學數學平均分數和優秀率都相同；勤奮程度和自覺性都一樣）。現隨機抽取甲、乙兩班各20名同學的上學期數學期末考試成績，得到莖葉圖如下：

（Ⅰ）依莖葉圖判斷哪個班的平均分高？
（Ⅱ）從乙班這20名同學中隨機抽取兩名高等數學成績不得低于85分的同學，求成績為90分的同學被抽中的概率；
（Ⅲ）學校規定：成績不低于85分的為優秀，請填寫下面的列聯表，并判斷“能否在犯錯誤的概率不超過0.025的前提下認為成績優秀與教學方式有關？”