
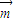 =(1,cos⊙x),
=(1,cos⊙x),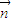 =(sin⊙x,
=(sin⊙x,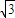 )(⊙>o),函數f(x)=
)(⊙>o),函數f(x)=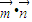 的圖象上一個最高點的坐標為(
的圖象上一個最高點的坐標為(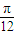 ,2),與之相鄰的一個最低點的坐標(
,2),與之相鄰的一個最低點的坐標(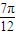 ,-2).
,-2). 口算題卡加應用題集訓系列答案
口算題卡加應用題集訓系列答案 綜合自測系列答案
綜合自測系列答案科目:高中數學 來源: 題型:
| AB |
| MB |
| BC |
| OM |
| CO |
| AB |
| a |
| b |
| e1 |
| e2 |
| 1 |
| 2 |
| 3 |
| 4 |
| a |
| b |
| a |
| b |
| a |
查看答案和解析>>
科目:高中數學 來源: 題型:
|
| α |
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
| m |
| n |
| AP |
| AO |
| AC |
| PA |
| PB |
| PC |
查看答案和解析>>
科目:高中數學 來源:2002年高中會考數學必備一本全2002年1月第1版 題型:044
如圖,已知△ABC的高AD、BE交于O點,連接CO.(1)用AC、BC、BO所示向量表示AO所示向量;(2)用向量證明:CO⊥A B.
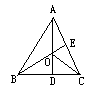
查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
| AB |
| MB |
| BC |
| OM |
| CO |
| AB |
| a |
| b |
| e1 |
| e2 |
| 1 |
| 2 |
| 3 |
| 4 |
| a |
| b |
| a |
| b |
| a |
| A.1個 | B.2個 | C.3個 | D.4個 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com