
某商場銷售某種商品的經驗表明,該商品每日的銷售量y (單位:千克)與銷售價格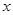 (單位:元/千克)滿足關系式y=
(單位:元/千克)滿足關系式y=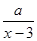 +10(x-6)2,其中3<x<6,a為常數.已知銷售價格為5元/千克時,每日可售出該商品11千克.
+10(x-6)2,其中3<x<6,a為常數.已知銷售價格為5元/千克時,每日可售出該商品11千克.
(1)求a的值;
(2)若該商品的成品為3元/千克, 試確定銷售價格x的值, 使商場每日銷售該商品所獲得的利潤最大.
(1) a=2 (2) 當銷售價格x=4時,商場每日銷售該商品所獲得的利潤最大,最大值為42.
解析試題分析:解:(1)由題設知x=5時y=11,則11=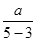 +10(5-6)2,解得a=2. 3分
+10(5-6)2,解得a=2. 3分
(2)由(1)知該商品每日的銷售量y=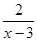 +10(x-6) 2,所以商場每日銷售該商品所獲得的利潤為
+10(x-6) 2,所以商場每日銷售該商品所獲得的利潤為
f(x)=(x-3) [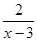 +10(x-6) 2]=2+10(x-3) (x-6) 2,3<x<6. 6分
+10(x-6) 2]=2+10(x-3) (x-6) 2,3<x<6. 6分
對函數f(x)求導,得f ′(x)=10[(x-6) 2+2(x-3)(x-6)]=30(x-4)(x-6).
令f ′(x)=0及3<x<6,解得x=4. 10分
當3<x<4時,f ′(x)>0,當4<x<6時,f ′(x)<0,于是有函數f(x)在(3,4)上遞增,在(4,6)上遞減,所以當x=4時函數f(x)取得最大值f(4)=42. 13分
答:當銷售價格x=4時,商場每日銷售該商品所獲得的利潤最大,最大值為42.
考點:函數的模型的運用
點評:解決的關鍵是對于已知中的利潤函數的 準確表示,然后借助于導數的知識來得到最值,屬于基礎題。


科目:高中數學 來源: 題型:解答題
某市居民自來水收費標準如下:每戶每月用水不超過4噸時,每噸為1.80元,當居民用水超過4噸時,超過部分每噸3.00元。若某月某用戶用水量為x噸,交水費為y元。
(1)求y關于x的函數關系
(2)若某用戶某月交水費為31.2元,求該用戶該月的用水量。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某地政府鑒于某種日常食品價格增長過快,欲將這種食品價格控制在適當范圍內,決定對這種食品生產廠家提供政府補貼,設這種食品的市場價格為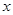 元/千克,政府補貼為
元/千克,政府補貼為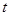 元/千克,根據市場調查,當
元/千克,根據市場調查,當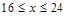 時,這種食品市場日供應量
時,這種食品市場日供應量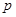 萬千克與市場日需量
萬千克與市場日需量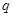 萬千克近似地滿足關系:
萬千克近似地滿足關系: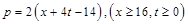 ,
,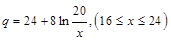 。當
。當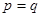 市場價格稱為市場平衡價格。
市場價格稱為市場平衡價格。
(1)將政府補貼表示為市場平衡價格的函數,并求出函數的值域;
(2)為使市場平衡價格不高于每千克20元,政府補貼至少為每千克多少元?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數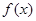 是定義在
是定義在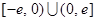 上的奇函數,當
上的奇函數,當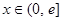 時,有
時,有 (其中
(其中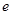 為自然對數的底,
為自然對數的底,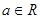 ).
).
(1)求函數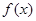 的解析式;
的解析式;
(2)設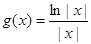 ,
,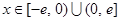 ,求證:當
,求證:當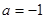 時,
時,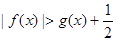 ;
;
(3)試問:是否存在實數 ,使得當
,使得當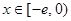 時,
時,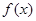 的最小值是3?如果存在,求出實數
的最小值是3?如果存在,求出實數 的值;如果不存在,請說明理由.
的值;如果不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
兩縣城A和B相距20km,現計劃在兩縣城外,以AB為直徑的半圓弧AB上選擇一點C建造垃圾處理廠,其對城市的影響度與所選地點到城市的距離有關,對城A和城B的總影響度為對城A與城B的影響度之和,記C點到城A的距離為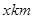 ,建在C處的垃圾處理廠對城A和城B的總影響度為
,建在C處的垃圾處理廠對城A和城B的總影響度為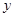 ,統計調查表明:垃圾處理廠對城A的影響度與所選地點到城A的距離的平方成反比,比例系數為4;對城B的影響度與所選地點到城B的距離的平方成反比,比例系數為k,當垃圾處理廠建在AB的中點時,對A和城B的總影響度為0.065。
,統計調查表明:垃圾處理廠對城A的影響度與所選地點到城A的距離的平方成反比,比例系數為4;對城B的影響度與所選地點到城B的距離的平方成反比,比例系數為k,當垃圾處理廠建在AB的中點時,對A和城B的總影響度為0.065。

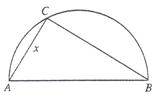
(1)將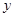 表示成
表示成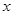 的函數;
的函數; (2)判斷弧AB上是否存在一點,使建在此處的垃圾處理廠對城A和城B的總影響度最小?若存在,求出該點到城A的距離;若不存在,說明理由。
(2)判斷弧AB上是否存在一點,使建在此處的垃圾處理廠對城A和城B的總影響度最小?若存在,求出該點到城A的距離;若不存在,說明理由。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(12分)某公司生產一種電子儀器的固定成本為20000元,每生產一臺儀器需增加投入100元,已知總收益滿足函數: ,其中
,其中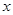 是儀器的月產量
是儀器的月產量
(1)將利潤 表示為月產量
表示為月產量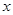 的函數
的函數
(2)當月產量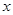 為何值時,公司所獲利潤最大?最大利潤是多少元?(總收益=總成本+利潤)
為何值時,公司所獲利潤最大?最大利潤是多少元?(總收益=總成本+利潤)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com