解:(1)因為y=f
2(x)-kx=1-x+
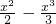
-kx,
所以y′=-1+x-x
2-k=-(x
2-x+k+1),
方程x
2-x+k+1=0的判別式△=(-1)
2-4(k+1)=-3-4k,
當k≥-

時,△≤0,y′=-(x
2-x+k+1)≤0,
故函數y=f
2(x)-kx在R上單調遞減;
當k<-

時,方程x
2-x+k+1=0的兩根為
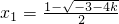
,

,
則x∈(-∞,x
1)時,y′<0,x∈(x
1,x
2)時,y′>0,x∈(x
2,+∞)時,y′<0,
故函數y=f
2(x)-kx(k∈R)的單調遞減區間為(-∞,x
1)和(x
2,+∞),單調遞增區間為(x
1,x
2);
(2)存在t=1,對于任意n∈N
*,關于x的方程f
n(x)=0在區間[t,t+1]上有唯一實數解,理由如下:
當n=1時,f
1(x)=1-x,令f
1(x)=1-x=0,解得x=1,
所以關于x的方程f
1(x)=0有唯一實數解x=1;
當n≥2時,由f
n(x)=1-x+

-

+…-
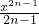
,
得f
n′(x)=-1+x-x
2+…+x
2n-3-x
2n-2,
若x=-1,則f′
n(x)=f′
n(-1)=-(2n-1)<0,
若x=0,則f′
n(x)=-1<0,
若x≠-1且x≠0時,則f′
n(x)=-
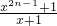
,
當x<-1時,x+1<0,x
2n-1+1<0,f′
n(x)<0,
當x>-1時,x+1>0,x
2n-1+1>0,f′
n(x)<0,
所以f′
n(x)<0,故f
n(x)在(-∞,+∞)上單調遞減.
因為f
n(1)=(1-1)+(

)+(

)+…+(
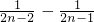
)>0,
f
n(2)=(1-2)+(
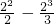
)+(
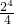
-
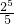
)+…+(
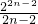
-
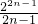
)
=-1+(

)•2
2+(
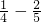
)•2
4+…+
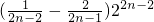
=-1-
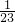
•2
2-
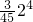
-…-

<0,
所以方程f
n(x)=0在[1,2]上有唯一實數解,
綜上所述,對于任意n∈N
*,關于x的方程f
n(x)=0在區間[1,2]上有唯一實數解,所以t=1.
分析:(1)y=f
2(x)-kx=1-x+
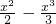
-kx,求導數y′,按△≤0,△>0兩種情況討論,△≤0時y′≤0,可知函數在R上的單調性;當△>0時解不等式y′>0,y′<0即得函數的單調區間;
(2)先求n=1時方程f
n(x)=0的根,得區間[1,2],理由如下:n=1時求出方程的根,易判斷;當n≥2時,求出f
n′(x),討論可得x=-1,0時f′
n(x)<0,x≠-1,0時,利用等比數列求和公式可化簡f′
n(x),此時也可判斷f′
n(x)<0,從而可得f
n(x)在(-∞,+∞)上單調遞減.而f
n(1)0,根據零點存在定理及函數單調性知,方程f
n(x)=0在[1,2]上有唯一實數解,綜述可得結論;
點評:本小題主要考查三次函數、一元二次不等式、一元二次方程、函數的零點、數列求和等基礎知識,考查數形結合、函數與方程、分類與整合、化歸與轉化的數學思想方法,以及抽象概括、推理論證、運算求解、創新意識.

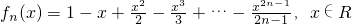 .
.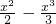 -kx,
-kx, 時,△≤0,y′=-(x2-x+k+1)≤0,
時,△≤0,y′=-(x2-x+k+1)≤0, 時,方程x2-x+k+1=0的兩根為
時,方程x2-x+k+1=0的兩根為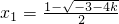 ,
, ,
, -
- +…-
+…-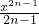 ,
,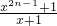 ,
, )+(
)+( )+…+(
)+…+(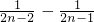 )>0,
)>0,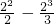 )+(
)+(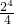 -
-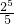 )+…+(
)+…+(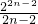 -
-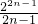 )
) )•22+(
)•22+(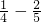 )•24+…+
)•24+…+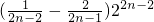
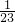 •22-
•22-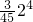 -…-
-…- <0,
<0,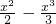 -kx,求導數y′,按△≤0,△>0兩種情況討論,△≤0時y′≤0,可知函數在R上的單調性;當△>0時解不等式y′>0,y′<0即得函數的單調區間;
-kx,求導數y′,按△≤0,△>0兩種情況討論,△≤0時y′≤0,可知函數在R上的單調性;當△>0時解不等式y′>0,y′<0即得函數的單調區間;

 對一切n∈N*均成立的最大實數a;
對一切n∈N*均成立的最大實數a;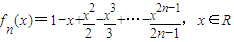 .
.