
某種項目的射擊比賽,開始時在距目標100m處射擊,如果命中記3分,且停止射擊;若第一次射擊未命中,可以進行第二次射擊,但目標已在150m處,這時命中記2分,且停止射擊;若第二次仍未命中,還可以進行第三次射擊,此時目標已在200m處,若第三次命中則記1分,并停止射擊;若三次都未命中,則記0分,且比賽結束.已知射手甲在100m處擊中目標的概率為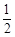 ,他的命中率與目標的距離的平方成反比,且各次射擊都是獨立的.
,他的命中率與目標的距離的平方成反比,且各次射擊都是獨立的.
(1)求射手甲在這次射擊比賽中命中目標的概率;
(2)求射手甲在這次射擊比賽中得分的數學期望.
(1)

 .
.
(2) .
.
【解析】本試題主要是考查了概率、獨立事件概率的乘法公式,以及對立事件的運用。
(1)根據已知條件,設出所求解的事件,然后利用獨立事件的乘法公式分情況討論,結合互斥事件的加法公式得到結論。
(2)根據隨機變量射手甲得分為X,根據得分的情況分別求解概率值,得到分布列和期望值。
解:記第一、二、三次射擊命中目標分別為事件 ,三次都未擊中目標為事件D,依題意
,三次都未擊中目標為事件D,依題意 ,設在
,設在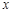 m處擊中目標的概率為
m處擊中目標的概率為 ,則
,則 ,且
,且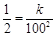 ,
,
 ,即
,即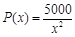 ,
。。。。。。。。。。
,
。。。。。。。。。。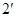
 ,
, ,
, .。。。。。。。。。。。。
.。。。。。。。。。。。。
(1) 由于各次射擊都是相互獨立的,
∴該射手在三次射擊中擊中目標的概率


 .
。。。。。
.
。。。。。
(2)依題意,設射手甲得分為X,則 ,
,
 ,
, ,
,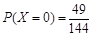 ,。。。。。。。
,。。。。。。。
 . 。。。。。。。。。。。。。。。。。。
. 。。。。。。。。。。。。。。。。。。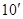


 口算題卡北京婦女兒童出版社系列答案
口算題卡北京婦女兒童出版社系列答案科目:高中數學 來源: 題型:
| 1 | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 | 2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com