
【題目】下列四個函數:①y=3﹣x;② ![]() ;③y=x2+2x﹣10;④
;③y=x2+2x﹣10;④  ,其中值域為R的函數有( )
,其中值域為R的函數有( )
A.1個
B.2個
C.3個
D.4個
【答案】B
【解析】解:根據一次函數的值域為R,y=3﹣x為一次函數,故①滿足條件;
根據x2+1≥1,可得 ![]() ,即函數
,即函數 ![]() 的值域為(0,1],故②不滿足條件;
的值域為(0,1],故②不滿足條件;
二次函數y=x2+2x﹣10的最小值為﹣11,無最大值,故函數y=x2+2x﹣10的值域為[﹣11,+∞),故③不滿足條件;
當x≤0時,y=﹣x≥0,當x>0時,y=﹣ ![]() <0,故函數
<0,故函數 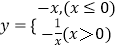 的值域為R,故④滿足條件;
的值域為R,故④滿足條件;
故選B
【考點精析】解答此題的關鍵在于理解函數的值域的相關知識,掌握求函數值域的方法和求函數最值的常用方法基本上是相同的.事實上,如果在函數的值域中存在一個最小(大)數,這個數就是函數的最小(大)值.因此求函數的最值與值域,其實質是相同的.


 階梯計算系列答案
階梯計算系列答案科目:高中數學 來源: 題型:
【題目】給出下列函數:①f(x)= ![]() ,g(x)=x+1;②f(x)=|x|,g(x)=
,g(x)=x+1;②f(x)=|x|,g(x)= ![]() ;③f(x)=x2﹣2x﹣1,g(t)=t2﹣2t﹣1.其中,是同一函數的是( )
;③f(x)=x2﹣2x﹣1,g(t)=t2﹣2t﹣1.其中,是同一函數的是( )
A.①②③
B.①③
C.②③
D.②
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在定義域內給定區間[a,b]上存在x0(a<x0<b)滿足f(x0)= ![]() ,則稱函數y=f(x)在區間[a,b]上的“平均值函數”,x0是它的一個均值點.若函數f(x)=﹣x2+mx+1是[﹣1,1]上的平均值函數,則實數m的取值范圍是
,則稱函數y=f(x)在區間[a,b]上的“平均值函數”,x0是它的一個均值點.若函數f(x)=﹣x2+mx+1是[﹣1,1]上的平均值函數,則實數m的取值范圍是
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定義在R的奇函數f(x)滿足當x>0時,f(x)=|2x﹣2|, 
(1)求函數f(x)的解析式;
(2)在圖中的坐標系中作出函數y=f(x)的圖象,并找出函數的單調區間;
(3)若集合{x|f(x)=a}恰有兩個元素,結合函數f(x)的圖象求實數a應滿足的條件.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列命題中正確的有( )
①命題x∈R,使sin x+cos x= ![]() 的否定是“對x∈R,恒有sin x+cos x≠
的否定是“對x∈R,恒有sin x+cos x≠ ![]() ”;
”;
②“a≠1或b≠2”是“a+b≠3”的充要條件;
③若曲線C上的所有點的坐標都滿足方程f(x,y)=0,則稱方程f(x,y)=0是曲線C的方程;
④十進制數66化為二進制數是1 000 010(2) .
A.①②③④
B.①④
C.②③
D.③④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖.已知等腰梯形ABCD中,AB∥CD,AD=AB=![]() CD,M是的CD的中點.N是AC與BM的交點,將△BCM沿BM向上翻折成△BPM,使平面BPM⊥平面ABMD
CD,M是的CD的中點.N是AC與BM的交點,將△BCM沿BM向上翻折成△BPM,使平面BPM⊥平面ABMD
(I)求證:AB⊥PN.
(Ⅱ)若E為PA的中點.求證:EN∥平面PDM.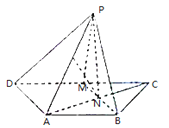
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com