已知函數(shù)f(x)=1n(2ax+1)+
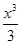
-x
2-2ax(a∈R).
(1)若y=f(x)在[4,+∞)上為增函數(shù),求實數(shù)a的取值范圍;
(2)當(dāng)a=
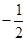
時,方程f(1-x)=
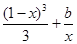
有實根,求實數(shù)b的最大值.
試題分析:(1)因為函數(shù)
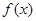
在
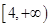
上為增函數(shù),所以
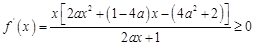
在
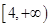
上恒成立。
①當(dāng)
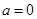
時,
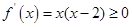
在
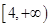
上恒成立,所以
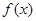
在
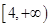
上為增
函數(shù),故
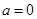
符合題意。
②當(dāng)
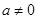
時,由函數(shù)
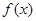
的定義域可知,必須有
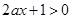
在
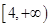
上恒成立,
故只能
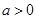
,所以
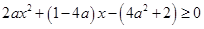
在
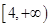
上恒成立。 .
令函數(shù)
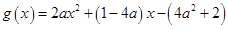
,其對稱軸為

,因為
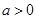
,
所以
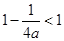
,要使
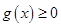
在
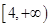
上恒成立,只要
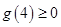
即可,即
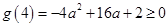
,所以
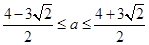
,因為
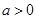
,所以
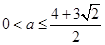
綜上所述,
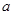
的取值范圍為
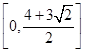
(2)當(dāng)
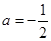
,方程
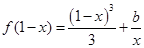
可化為
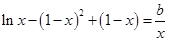
。問題轉(zhuǎn)
化為
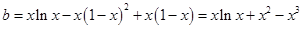
在
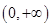
上有解,即求函數(shù)


的值域。令函數(shù)
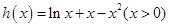
則
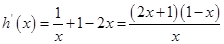
,所以當(dāng)
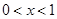
時,
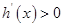
,函數(shù)
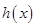
在
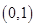
上為增函數(shù),當(dāng)
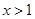
時,
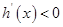
,函數(shù)
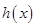
在
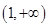
上為減函數(shù),因此
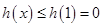
。而
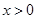
,所以
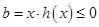
,因此當(dāng)
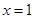
時,
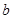
取到最大值

.
點評:本題主要考查了利用函數(shù)的導(dǎo)數(shù)求解函數(shù)極值的應(yīng)用,及利用函數(shù)的導(dǎo)數(shù)研究函數(shù)的單調(diào)性及函數(shù)的最值的求解,解答本題要求考生具備較強(qiáng)的邏輯推理與運算的能力.
練習(xí)冊系列答案
相關(guān)習(xí)題
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
設(shè)
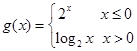
,則
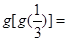 __________
__________.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
已知函數(shù)
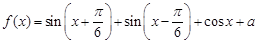
的最大值為1.
(1)求常數(shù)
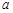
的值;(2)求使
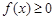
成立的
x的取值集合.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
已知函數(shù)
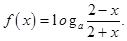
.
求(1)
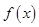
的定義域;
(2)判斷
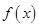
在其定義域上的奇偶性,并予以證明,
(3)求
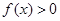
的解集。
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
已知函數(shù)
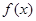
和
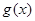
都是定義在
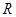
上的奇函數(shù),設(shè)
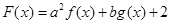
,若
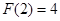
,則
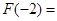
.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
已知函數(shù)
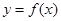
是定義在
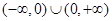
上的奇函數(shù),當(dāng)
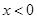
時,
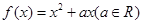
,且
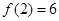
。
(1)求
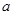
的值,(2)求

的值.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
已知定義在實數(shù)集上的函數(shù)
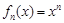
,
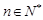
,其導(dǎo)函數(shù)記為
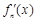
,
(1)設(shè)函數(shù)
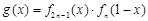
,求
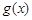
的極大值與極小值;
(2)試求關(guān)于
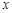
的方程
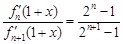
在區(qū)間
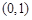
上的實數(shù)根的個數(shù)。
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
定義在[-1,1]上的奇函數(shù)
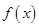
滿足
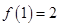
,且當(dāng)
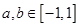
,
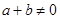
時,有
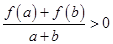
.
(1)試問函數(shù)
f(
x)的圖象上是否存在兩個不同的點
A,
B,使直線
AB恰好與
y軸垂直,若存在,求出
A,
B兩點的坐標(biāo);若不存在,請說明理由并加以證明.
(2)若
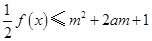
對所有
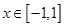
,
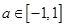
恒成立,
求實數(shù)
m的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
建造一間占 地面積為12m²的背面靠墻的豬圈,底面為長方形,豬圈正面的造價為每平方米12元,側(cè)面的造價為每平方米80元,屋頂造價為1120元.如果墻高3m,且不計豬圈背面的費用,問:如何設(shè)計能使豬圈的總 造價最低?最低總造價是多少?
查看答案和解析>>

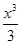 -x2-2ax(a∈R).
-x2-2ax(a∈R).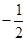 時,方程f(1-x)=
時,方程f(1-x)=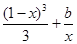 有實根,求實數(shù)b的最大值.
有實根,求實數(shù)b的最大值.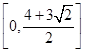 (2)
(2)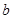 取到最大值
取到最大值
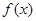 在
在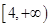 上為增函數(shù),所以
上為增函數(shù),所以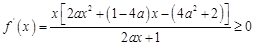
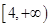 上恒成立。
上恒成立。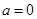 時,
時,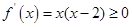 在
在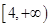 上恒成立,所以
上恒成立,所以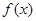 在
在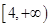 上為增
上為增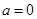 符合題意。
符合題意。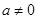 時,由函數(shù)
時,由函數(shù)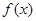 的定義域可知,必須有
的定義域可知,必須有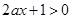 在
在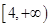 上恒成立,
上恒成立,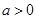 ,所以
,所以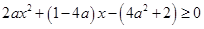 在
在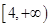 上恒成立。 .
上恒成立。 .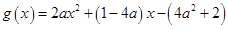 ,其對稱軸為
,其對稱軸為 ,因為
,因為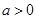 ,
,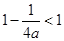 ,要使
,要使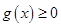 在
在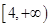 上恒成立,只要
上恒成立,只要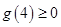 即可,即
即可,即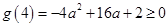 ,所以
,所以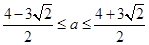 ,因為
,因為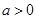 ,所以
,所以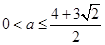
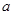 的取值范圍為
的取值范圍為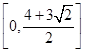
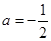 ,方程
,方程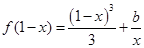 可化為
可化為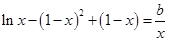 。問題轉(zhuǎn)
。問題轉(zhuǎn)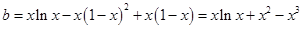 在
在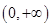 上有解,即求函數(shù)
上有解,即求函數(shù)
 的值域。令函數(shù)
的值域。令函數(shù)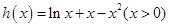
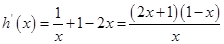 ,所以當(dāng)
,所以當(dāng)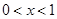 時,
時,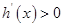 ,函數(shù)
,函數(shù)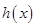 在
在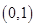 上為增函數(shù),當(dāng)
上為增函數(shù),當(dāng)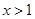 時,
時,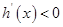 ,函數(shù)
,函數(shù)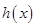 在
在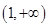 上為減函數(shù),因此
上為減函數(shù),因此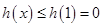 。而
。而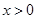 ,所以
,所以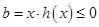 ,因此當(dāng)
,因此當(dāng)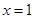 時,
時,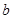 取到最大值
取到最大值 .
.

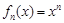 ,
,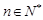 ,其導(dǎo)函數(shù)記為
,其導(dǎo)函數(shù)記為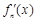 ,
,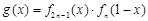 ,求
,求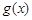 的極大值與極小值;
的極大值與極小值;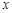 的方程
的方程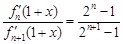 在區(qū)間
在區(qū)間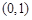 上的實數(shù)根的個數(shù)。
上的實數(shù)根的個數(shù)。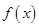 滿足
滿足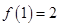 ,且當(dāng)
,且當(dāng)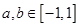 ,
,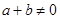 時,有
時,有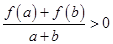 .
.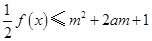 對所有
對所有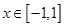 ,
,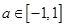 恒成立,
恒成立,