
33.(2009湖南卷理)(本小題滿分13分)
在平面直角坐標系xOy中,點P到點F(3,0)的距離的4倍與它到直線x=2的距離的3倍之和記為d,當P點運動時,d恒等于點P的橫坐標與18之和
(Ⅰ)求點P的軌跡C;
(Ⅱ)設過點F的直線I與軌跡C相交于M,N兩點,求線段MN長度的最大值。
解(Ⅰ)設點P的坐標為(x,y),則![]() 3︳x-2︳
3︳x-2︳
由題設
當x>2時,由①得![]()
化簡得 ![]()
當![]() 時 由①得
時 由①得![]()
化簡得![]()
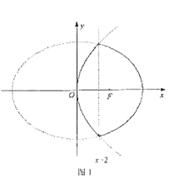
 故點P的軌跡C是橢圓
故點P的軌跡C是橢圓![]() 在直線x=2的右側(cè)部分與拋物線
在直線x=2的右側(cè)部分與拋物線![]() 在直線x=2的左側(cè)部分(包括它與直線x=2的交點)所組成的曲線,參見圖1
在直線x=2的左側(cè)部分(包括它與直線x=2的交點)所組成的曲線,參見圖1
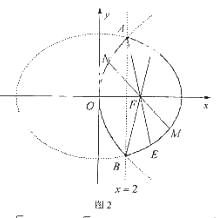
(Ⅱ)如圖2所示,易知直線x=2與![]() ,
,![]() 的交點都是A(2,
的交點都是A(2,![]() ),
),
B(2,![]() ),直線AF,BF的斜率分別為
),直線AF,BF的斜率分別為![]() =
=![]() ,
,![]() =
=![]() .
.
當點P在![]() 上時,由②知
上時,由②知
![]() . ④
. ④
當點P在![]() 上時,由③知
上時,由③知
![]() ⑤
⑤
若直線l的斜率k存在,則直線l的方程為![]()
(i)當k≤![]() ,或k≥
,或k≥![]() ,即k≤-2
,即k≤-2 ![]() 時,直線I與軌跡C的兩個交點M(
時,直線I與軌跡C的兩個交點M(![]() ,
,![]() ),N(
),N(![]() ,
,![]() )都在C
)都在C ![]() 上,此時由④知
上,此時由④知
∣MF∣= 6 - ![]()
![]() ∣NF∣= 6 -
∣NF∣= 6 - ![]()
![]()
從而∣MN∣= ∣MF∣+ ∣NF∣= (6 - ![]()
![]() )+ (6 -
)+ (6 - ![]()
![]() )=12 -
)=12 - ![]() (
( ![]() +
+![]() )
)
由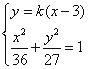 得
得![]() 則
則![]() ,
,![]() 是這個方程的兩根,所以
是這個方程的兩根,所以![]() +
+![]() =
=![]() *∣MN∣=12 -
*∣MN∣=12 - ![]() (
(![]() +
+![]() )=12 -
)=12 - ![]()
因為當![]()
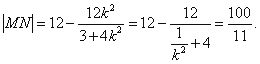
當且僅當![]() 時,等號成立。
時,等號成立。
(2)當![]() 時,直線L與軌跡C的兩個交點
時,直線L與軌跡C的兩個交點![]() 分別在
分別在![]() 上,不妨設點
上,不妨設點![]() 在
在![]() 上,點
上,點![]() 上,則④⑤知,
上,則④⑤知,![]()
設直線AF與橢圓![]() 的另一交點為E
的另一交點為E![]()
![]()
所以![]() 。而點A,E都在
。而點A,E都在![]() 上,且
上,且
![]() 有(1)知
有(1)知![]()
若直線![]() 的斜率不存在,則
的斜率不存在,則![]() =
=![]() =3,此時
=3,此時
![]()
綜上所述,線段MN長度的最大值為![]()


 周周清檢測系列答案
周周清檢測系列答案 輕巧奪冠周測月考直通高考系列答案
輕巧奪冠周測月考直通高考系列答案科目:高中數(shù)學 來源: 題型:
(2009湖南卷理)從10名大學生畢業(yè)生中選3個人擔任村長助理,則甲、乙至少有1人入選,而丙沒有入選的不同選法的種數(shù)位 ![]()
![]() [ ]
[ ]
A 85 B
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
(2009湖南卷理)設函數(shù)![]() 在(
在(![]() ,+
,+![]() )內(nèi)有定義。對于給定的正數(shù)K,定義函數(shù)
)內(nèi)有定義。對于給定的正數(shù)K,定義函數(shù)
![]()
取函數(shù)![]() =
=![]() 。若對任意的
。若對任意的![]() ,恒有
,恒有![]() =
=![]() ,則
,則 ![]()
![]()
A.K的最大值為2 B. K的最小值為2
C.K的最大值為1 D. K的最小值為1 【 】
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
(2009湖南卷理)將正ABC分割成![]()
![]() (
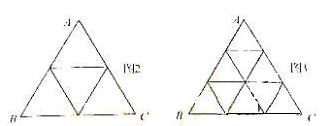
(![]() ≥2,n∈N)個全等的小正三角形(圖2,圖3分別給出了n=2,3的情形),在每個三角形的頂點各放置一個數(shù),使位于ABC的三遍及平行于某邊的任一直線上的數(shù)(當數(shù)的個數(shù)不少于3時)都分別一次成等差數(shù)列,若頂點A ,B ,C處的三個數(shù)互不相同且和為1,記所有頂點上的數(shù)之和為f(n),則有f(2)=2,f(3)= ,…,
≥2,n∈N)個全等的小正三角形(圖2,圖3分別給出了n=2,3的情形),在每個三角形的頂點各放置一個數(shù),使位于ABC的三遍及平行于某邊的任一直線上的數(shù)(當數(shù)的個數(shù)不少于3時)都分別一次成等差數(shù)列,若頂點A ,B ,C處的三個數(shù)互不相同且和為1,記所有頂點上的數(shù)之和為f(n),則有f(2)=2,f(3)= ,…,

查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
(2009湖南卷理)(本小題滿分12分)
為拉動經(jīng)濟增長,某市決定新建一批重點工程,分別為基礎(chǔ)設施工程、民生工程和產(chǎn)業(yè)建設工程三類,這三類工程所含項目的個數(shù)分別占總數(shù)的.![]() 、
、![]() 、
、![]() ,現(xiàn)在3名工人獨立地從中任選一個項目參與建設。
,現(xiàn)在3名工人獨立地從中任選一個項目參與建設。 ![]()
![]()
(I)求他們選擇的項目所屬類別互不相同的概率;
(II)記![]() 為3人中選擇的項目屬于基礎(chǔ)設施工程、民生工程和產(chǎn)業(yè)建設工程的人數(shù),求
為3人中選擇的項目屬于基礎(chǔ)設施工程、民生工程和產(chǎn)業(yè)建設工程的人數(shù),求![]() 的分布列及數(shù)學期望。
的分布列及數(shù)學期望。
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
(2009湖南卷理)(本小題滿分12分)
如圖4,在正三棱柱![]() 中,
中,![]()
D是![]() 的中點,點E在
的中點,點E在![]() 上,且
上,且![]() 。
。
(I) 證明平面![]() 平面
平面![]()
(II) 求直線![]() 和平面
和平面![]() 所成角的正弦值。
所成角的正弦值。 ![]()
![]()

查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com