
分析 (1)利用兩個向量的坐標形式的運算,兩個向量的數量積公式,求得($\overrightarrow{a}$+$\overrightarrow{b}$)•($\overrightarrow{a}$-$\overrightarrow{b}$)=0,可得($\overrightarrow{a}$+$\overrightarrow{b}$)⊥($\overrightarrow{a}$-$\overrightarrow{b}$).
(2)由條件求得$\overrightarrow{a}•\overrightarrow{b}$=0,即sin(α-$\frac{π}{6}$)=0,結合0≤a≤2π,求得α的值.
解答 解:(1)∵向量$\overrightarrow{a}$=(cosα,sinα)(0≤a≤2π),$\overrightarrow{b}$=(-$\frac{1}{2},\frac{\sqrt{3}}{2}$),
∴|$\overrightarrow{a}$|=|$\overrightarrow{b}$|,($\overrightarrow{a}$+$\overrightarrow{b}$)•($\overrightarrow{a}$-$\overrightarrow{b}$)=${\overrightarrow{a}}^{2}$-${\overrightarrow{b}}^{2}$=0,∴($\overrightarrow{a}$+$\overrightarrow{b}$)⊥($\overrightarrow{a}$-$\overrightarrow{b}$).
(2)∵已知兩個向量$\sqrt{3}$$\overrightarrow{a}$+$\overrightarrow{b}$與$\overrightarrow{a}$-$\sqrt{3}$$\overrightarrow{b}$的模相等,
∴${(\sqrt{3}\overrightarrow{a}+\overrightarrow{b})}^{2}$=${(\overrightarrow{a}-\sqrt{3}\overrightarrow{b})}^{2}$,∴3${\overrightarrow{a}}^{2}$+${\overrightarrow{b}}^{2}$+2$\sqrt{3}$•$\overrightarrow{a}•\overrightarrow{b}$=${\overrightarrow{a}}^{2}$+3${\overrightarrow{b}}^{2}$-2$\sqrt{3}$•$\overrightarrow{a}•\overrightarrow{b}$,
再結合|$\overrightarrow{a}$|=|$\overrightarrow{b}$|,可得$\overrightarrow{a}•\overrightarrow{b}$=0,即$\frac{\sqrt{3}}{2}sinα$-$\frac{1}{2}$cosα=sin(α-$\frac{π}{6}$)=0,
∴α-$\frac{π}{6}$=kπ,k∈Z.
∵0≤a≤2π,∴α=$\frac{π}{6}$,或α=$\frac{7π}{6}$.
點評 本題主要考查兩個向量垂直的判定,兩個向量的坐標形式的運算,兩個向量的數量積公式的應用,屬于中檔題.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (0,$\frac{1}{4}$) | B. | ($\frac{1}{4}$,$\frac{1}{2}$) | C. | ($\frac{1}{2}$,$\frac{3}{4}$) | D. | ($\frac{3}{4}$,1) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -$\sqrt{3}$ | B. | -$\frac{\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
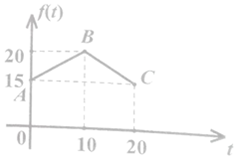 經過市場調查,某門市部的一種小商品在過去的20天內的銷售量(件)與價格(元)均為時間t (天)的函數,且日銷售量近似滿足g(t)=80-2t (件),而日銷售量價格近似滿足函數f(t),且f(t)的圖象為如圖所示的兩線段AB,BC.
經過市場調查,某門市部的一種小商品在過去的20天內的銷售量(件)與價格(元)均為時間t (天)的函數,且日銷售量近似滿足g(t)=80-2t (件),而日銷售量價格近似滿足函數f(t),且f(t)的圖象為如圖所示的兩線段AB,BC.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com