
【題目】下列四個命題中,正確的是( )
A.奇函數的圖象一定過原點
B.y=x2+1(﹣4<x≤4)是偶函數
C.y=|x+1|﹣|x﹣1|是奇函數
D.y=x+1是奇函數
【答案】C
【解析】解:根據題意,依次分析選項:
對于A、當奇函數的定義域不含有0時,其圖象不過原點,如y= ![]() ,故A錯誤;
,故A錯誤;
對于B、y=x2+1(﹣4<x≤4),其定義域不關于原點對稱,不是偶函數,故B錯誤;
對于C、y=|x+1|﹣|x﹣1|= 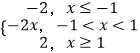 ,分析可得有f(﹣x)=﹣f(x),為奇函數,故C正確;
,分析可得有f(﹣x)=﹣f(x),為奇函數,故C正確;
對于D、對于函數y=x+1,f(﹣x)=﹣f(x)不成立,不是奇函數,故D錯誤;
故選:C.
【考點精析】解答此題的關鍵在于理解命題的真假判斷與應用的相關知識,掌握兩個命題互為逆否命題,它們有相同的真假性;兩個命題為互逆命題或互否命題,它們的真假性沒有關系,以及對函數奇偶性的性質的理解,了解在公共定義域內,偶函數的加減乘除仍為偶函數;奇函數的加減仍為奇函數;奇數個奇函數的乘除認為奇函數;偶數個奇函數的乘除為偶函數;一奇一偶的乘積是奇函數;復合函數的奇偶性:一個為偶就為偶,兩個為奇才為奇.


科目:高中數學 來源: 題型:
【題目】設函數f(x)的定義域為R,若存在常數M>0,使得|f(x)|≤M|x|對一切的實數x都成立,則稱f(x)為“倍約束函數”.現給出下列函數: ①f(x)=2x,
②f(x)=x2+1,
③f(x)=sinx+cosx,
④f(x)= ![]() ,
,
⑤f(x)是定義在實數集上的奇函數,且對一切的x1 , x2均有|f(x1)﹣f(x2)|≤2|x1﹣x2|.
其中是“倍約束函數”的有( )
A.1個
B.2個
C.3個
D.4個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義在[﹣1,1]上的奇函數f(x)滿足當0<x≤1時,f(x)= ![]() ,
,
(1)求f(x)在[﹣1,1]上的解析式;
(2)判斷并證明f(x)在[﹣1,0)上的單調性;
(3)當x∈(0,1]時,方程 ![]() ﹣2x﹣m=0有解,試求實數m的取值范圍.
﹣2x﹣m=0有解,試求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四邊形ABCD中,AB=AD=CD=1,BD= ![]() ,BD⊥CD.將四邊形ABCD沿對角線BD折成四面體A′﹣BCD,使平面A′BD⊥平面BCD,則下列結論正確的是( )
,BD⊥CD.將四邊形ABCD沿對角線BD折成四面體A′﹣BCD,使平面A′BD⊥平面BCD,則下列結論正確的是( ) 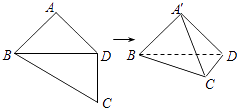
A.A′C⊥BD
B.∠BA′C=90°
C.CA′與平面A′BD所成的角為30°
D.四面體A′﹣BCD的體積為 ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知命題p: ![]() ,命題q:x∈R,x2﹣2ax+2﹣a=0,若命題“p∧q”是真命題,則實數a的取值范圍是( )
,命題q:x∈R,x2﹣2ax+2﹣a=0,若命題“p∧q”是真命題,則實數a的取值范圍是( )
A.(﹣∞,﹣2]∪{1}
B.(﹣∞,﹣2]∪[1,2]
C.[1,+∞)
D.[﹣2,1]
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知雙曲線的中心在原點,焦點F1 , F2在坐標軸上,離心率為 ![]() ,且過點(4,﹣
,且過點(4,﹣ ![]() ),點M(3,m)在雙曲線上.
),點M(3,m)在雙曲線上.
(1)求雙曲線方程;
(2)求證:MF1⊥MF2;
(3)求△F1MF2的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,已知圓C1:x2+y2=16和圓C2:(x﹣7)2+(y﹣4)2=4,
(1)求過點(4,6)的圓C1的切線方程;
(2)設P為坐標平面上的點,且滿足:存在過點P的無窮多對互相垂直的直線l1和l2 , 它們分別與圓C1和圓C2相交,且直線l1被圓C1截得的弦長是直線l2被圓C2截得的弦長的2倍.試求所有滿足條件的點P的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知雙曲線 ![]() 的左、右焦點分別為F1、F2 , P為C的右支上一點,且|PF2|=|F1F2|,則
的左、右焦點分別為F1、F2 , P為C的右支上一點,且|PF2|=|F1F2|,則 ![]() 等于( )
等于( )
A.24
B.48
C.50
D.56
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com