③④⑤
分析:對于①,由于函數y=sin|x|不是周期函數,故排除之.對于②,由題意知對于二次函數y=x
2-ax+1,應有△=a
2-4>0,解得a的范圍即可進行判斷;對于③,若函數f(x)對任意x∈R都有f(x)=-f(2-x),則 f(x)+f(2-x)=0.再由f(x)的最小正周期為3,可得f(x)的圖象關于點(1,0)對稱,故③正確.對于④,將極坐標方程 4sin
2θ=3 化成直角坐標方程后判斷.⑤先畫出函數
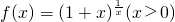
的圖象,從圖象上觀察可知.
解答:
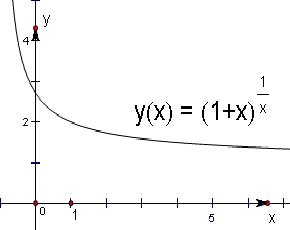
解:由于函數y=sin|x|不是周期函數,故排除①.
若函數
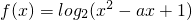
的值域為R,則對于二次函數y=x
2-ax+1,應有△=a
2-4>0,解得 a<-2,或 a>2,故排除②.
若函數f(x)對任意x∈R都有f(x)=-f(2-x),則 f(x)+f(2-x)=0.再由f(x)的最小正周期為3,可得 f(x-3)+f(2-x)=0.
由于
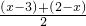
=-

,故f(x)的圖象關于點(1,0)對稱,故③正確.
由于極坐標方程 4sin
2θ=3 即 4ρ
2sin
2θ=3ρ
2,即 4y
2=3(x
2+y
2),即 y=±

x,故表示的圖形是兩條相交直線,故④正確.
⑤如圖,從函數
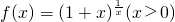
的圖象上觀察可知,當x>0時,其最大值不超過3,
故當M>3時,即存在無數多個正實數M,使得|f(x)|≤M成立;故⑤正確.
其中真命題的序號是 ③④⑤.
故答案為:③④⑤.
點評:本小題主要考查命題的真假判斷與應用、函數周期性的應用、不等式的解法等基礎知識,考查運算求解能力,考查數形結合思想、化歸與轉化思想.屬于基礎題.

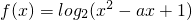 的值域為R,則-2<a<2;
的值域為R,則-2<a<2;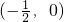 對稱;
對稱;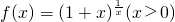 ,則存在無數多個正實數M,使得|f(x)|≤M成立;
,則存在無數多個正實數M,使得|f(x)|≤M成立;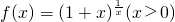 的圖象,從圖象上觀察可知.
的圖象,從圖象上觀察可知.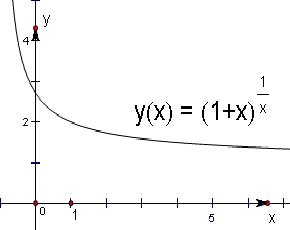 解:由于函數y=sin|x|不是周期函數,故排除①.
解:由于函數y=sin|x|不是周期函數,故排除①.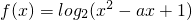 的值域為R,則對于二次函數y=x2-ax+1,應有△=a2-4>0,解得 a<-2,或 a>2,故排除②.
的值域為R,則對于二次函數y=x2-ax+1,應有△=a2-4>0,解得 a<-2,或 a>2,故排除②.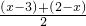 =-
=- ,故f(x)的圖象關于點(1,0)對稱,故③正確.
,故f(x)的圖象關于點(1,0)對稱,故③正確. x,故表示的圖形是兩條相交直線,故④正確.
x,故表示的圖形是兩條相交直線,故④正確.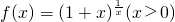 的圖象上觀察可知,當x>0時,其最大值不超過3,
的圖象上觀察可知,當x>0時,其最大值不超過3,
