①函數y=f(-x+2)與y=f(x-2)的圖象關于y軸對稱;
②用二分法求函數f(x)=lnx+x-2在(1,2)上零點的近似值,要求精確度0.1,則至少需要五次對對應區間中點的函數值的計算;
③函數f(x)(其中f(x)恒不等于0)滿足 f(x)=f(x+1)f(x-1),則f(2013)f(0)=1;
④若f(1-x)=-f(x+1),則函數y=f(x-1)的圖象關于點(2,0)對稱.
其中正確命題的序號是( )
A.①③④
B.②③④
C.①②
D.③④
【答案】
分析:根據函數的對稱性判斷①;原來區間的長度等于1,每經過一次操作,區間長度變為原來的一半,經過n此操作后,區間長度變為
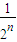
,由此能判斷②;函數f(x)(其中f(x)恒不等于0)滿足 f(x)=f(x+1)f(x-1),則f(2013)f(0)=1,由此能判斷③;若f(1-x)=-f(x+1),(x+1)+f(1-x)=0恒成立,則函數y=f(x)的圖象關于(1,0)點對稱,由此能判斷④.
解答:解:①函數y=f (-x+2)與y=f (x-2)的圖象關于x=2軸對稱,故①不正確;
②開區間(1,2)的長度等于1,每經過一次操作,區間長度變為原來的一半,經過n此操作后,
區間長度變為
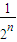
,故有
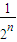
≤0.1,
∴n≥4,
∴至少需要操作4次.
故②不正確;
③函數f(x)(其中f(x)恒不等于0)滿足 f(x)=f(x+1)f(x-1),則f(2013)f(0)=1,
故③正確;
④若f(1-x)=-f(x+1),(x+1)+f(1-x)=0恒成立,則函數y=f(x)的圖象關于(1,0)點對稱,
∴函數y=f(x-1)的圖象關于點(2,0)對稱,故④正確;
故選D.
點評:本題考查命題的真假判斷與應用,解題時要認真審題,仔細解答,注意函數的對稱性、周期性、奇偶性的應用.

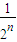 ,由此能判斷②;函數f(x)(其中f(x)恒不等于0)滿足 f(x)=f(x+1)f(x-1),則f(2013)f(0)=1,由此能判斷③;若f(1-x)=-f(x+1),(x+1)+f(1-x)=0恒成立,則函數y=f(x)的圖象關于(1,0)點對稱,由此能判斷④.
,由此能判斷②;函數f(x)(其中f(x)恒不等于0)滿足 f(x)=f(x+1)f(x-1),則f(2013)f(0)=1,由此能判斷③;若f(1-x)=-f(x+1),(x+1)+f(1-x)=0恒成立,則函數y=f(x)的圖象關于(1,0)點對稱,由此能判斷④.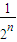 ,故有
,故有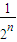 ≤0.1,
≤0.1,

 名校課堂系列答案
名校課堂系列答案