分析:(1)過點N,作NP∥CC
1,可得NP∥平面BCC
1B
1 ,且
=
.由條件可得
=
,故有
=
,可得PM∥AD,故 PM∥BC.可得MP∥
平面BCC
1B
1 ,可得平面MNP∥平面BCC
1B
1 .從而證得MN∥平面BCC
1B
1.
(2)由三角形相似求得 MP=
(1-
),NP=
x,可得函數y=f(x)=
=
,(0<x<2).
(3)由(2)可得,當x=1時,MN最短為1,此時,M、N分別為AC、DC
1的中點,MN與AC所成的角即為∠NMC.求得MP、NP、MN的值,可得∠NMC 的值,
即為所求.
解答: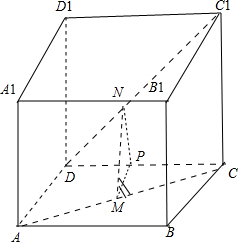
解:(1)過點N,作NP∥CC
1,則由CC
1?平面BCC
1B
1,NP不在平面平面BCC
1B
1 內,
可得NP∥平面BCC
1B
1 ,且
=
.
∵AM=DN,AC=DC
1,∴CP=CM,∴
=
.
故有
=
,∴PM∥AD,PM∥BC.
再由BC?平面BCC
1B
1,NP不在平面平面BCC
1B
1 內,可得MP∥平面BCC
1B
1 ,
再由MP∩NP=P,可得平面MNP∥平面BCC
1B
1 .
再由MN不在平面BCC
1B
1內,可得MN∥面BCC
1B
1 .
(2)由(1)可得三角形MNP為直角三角形,設MN=y,由于AM=DN=x,正方體ABCD-A
1B
1C
1D
1中棱長為
,
由
=
,可得
=,∴MP=
(1-
),且0<x<2.
由
=
可得
=,NP=
x.
故函數y=f(x)=
=
=
,(0<x<2).
(3)由(2)可得,當x=1時,MN最短為1,此時,M、N分別為AC、DC
1的中點,
MN與AC所成的角即為∠NMC.
由于此時,MC=
=1=NC,MN=
=1,故△MNC為等邊三角形,故∠NMC=
,
即MN與AC所成的角等于
.
點評:本題主要考查直線和平面平行的判定定理的應用,求兩條直線所成的角,屬于中檔題.

 解:(1)過點N,作NP∥CC1,則由CC1?平面BCC1B1,NP不在平面平面BCC1B1 內,
解:(1)過點N,作NP∥CC1,則由CC1?平面BCC1B1,NP不在平面平面BCC1B1 內,

 如圖是從上下底面處在水平狀態下的棱長為a的正方體ABCD-A1B1C1D1中分離出來的:
如圖是從上下底面處在水平狀態下的棱長為a的正方體ABCD-A1B1C1D1中分離出來的: 已知邊長為6的正方體ABCD-A1B1C1D1,E,F為AD、CD上靠近D的三等分點,H為BB1上靠近B的三等分點,G是EF的中點.
已知邊長為6的正方體ABCD-A1B1C1D1,E,F為AD、CD上靠近D的三等分點,H為BB1上靠近B的三等分點,G是EF的中點. 如圖所示,在棱長為2cm的正方體ABCD-A1B1C1D1中,A1B1的中點是P,過點A1作出與截面PBC1平行的截面,簡單證明截面形狀,并求該截面的面積.
如圖所示,在棱長為2cm的正方體ABCD-A1B1C1D1中,A1B1的中點是P,過點A1作出與截面PBC1平行的截面,簡單證明截面形狀,并求該截面的面積.