
 (*),其中n、m、r∈N*,r≤m<n且r≤n-m.某同學用概率論方法證明等式(*)如下:
(*),其中n、m、r∈N*,r≤m<n且r≤n-m.某同學用概率論方法證明等式(*)如下: ,k=0,1,2,…,r.
,k=0,1,2,…,r. ,
, ,即等式(*)成立.
,即等式(*)成立. 種情況,又從中隨機取出r件產品,共有
種情況,又從中隨機取出r件產品,共有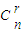 種情況,k=0,1,…,r,故其概率為
種情況,k=0,1,…,r,故其概率為 ,k=0,1,…,r.
,k=0,1,…,r.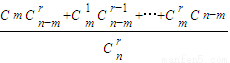 ,
,

科目:高中數學 來源: 題型:
| C | 0 m |
| C | r n-m |
| C | 1 m |
| C | r-1 n-m |
| C | r m |
| C | 0 n-m |
| C | r n |
| ||||
|
| ||||||||||||
|
| C | 0 m |
| C | r n-m |
| C | 1 m |
| C | r-1 n-m |
| C | r m |
| C | 0 n-m |
| C | r n |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
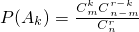 ,k=0,1,…,r.顯然A0,A1,…,Ar為互斥事件,且A0∪A1∪…∪Ar=Ω(必然事件),因此1=P(Ω)=P(A0)+P(A1)+…P(Ar)=
,k=0,1,…,r.顯然A0,A1,…,Ar為互斥事件,且A0∪A1∪…∪Ar=Ω(必然事件),因此1=P(Ω)=P(A0)+P(A1)+…P(Ar)=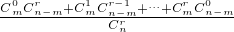 ,所以Cm0Cn-mr+Cm1Cn-mr-1+…+CmrCn-m0=Cnr,即等式(*)成立.對此,有的同學認為上述證明是正確的,體現了偶然性與必然性的統一;但有的同學對上述證明方法的科學性與嚴謹性提出質疑.現有以下四個判斷:
,所以Cm0Cn-mr+Cm1Cn-mr-1+…+CmrCn-m0=Cnr,即等式(*)成立.對此,有的同學認為上述證明是正確的,體現了偶然性與必然性的統一;但有的同學對上述證明方法的科學性與嚴謹性提出質疑.現有以下四個判斷:查看答案和解析>>
科目:高中數學 來源:福建模擬 題型:填空題
| C | 0m |
| C | rn-m |
| C | 1m |
| C | r-1n-m |
| C | rm |
| C | 0n-m |
| C | rn |
| ||||
|
| ||||||||||||
|
| C | 0m |
| C | rn-m |
| C | 1m |
| C | r-1n-m |
| C | rm |
| C | 0n-m |
| C | rn |
查看答案和解析>>
科目:高中數學 來源:福建省模擬題 題型:填空題
 (*)
(*) ,k=0,1,…,r。顯然A0,A1,…,Ar為互斥事件,且
,k=0,1,…,r。顯然A0,A1,…,Ar為互斥事件,且 (必然事件),因此
(必然事件),因此
 ,
, ,即等式(*)成立。
,即等式(*)成立。查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com