
【題目】已知a,b,c均為正數,設函數f(x)=|x﹣b|﹣|x+c|+a,x∈R.
(1)若a=2b=2c=2,求不等式f(x)<3的解集;
(2)若函數f(x)的最大值為1,證明:![]() .
.
【答案】(1)![]() .(2)見解析
.(2)見解析
【解析】
(1)根據a=2b=2c=2時,將不等式f(x)<3化為|x﹣1|﹣|x+1|<1,然后利用零點分段法解不等式即可;
(2)根據條件利用絕對值三角不等式,可得a+b+c=1,然后利用柯西不等式,即可證明![]() .
.
(1)當a=2b=2c=2時,a=2,b=c=1
不等式f(x)<3化為|x﹣1|﹣|x+1|<1,
當x≤﹣1時,原不等式化為1﹣x+1+x<1,解集為;
當﹣1<x<1時,原不等式化為1﹣x﹣x﹣1<1,解得![]() ;
;
當x≥1時,原不等式化為x﹣1﹣x﹣1<1,解得x≥1,
∴不等式f(x)<3的解集為![]() .
.
(2)∵![]()
又∵a,b,c>0,
∴![]()
∴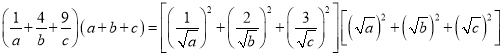
![]()
![]()
當且僅當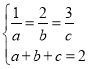 ,即
,即![]() 時等號成立,
時等號成立,
∴![]() .
.


 新題型全程檢測期末沖刺100分系列答案
新題型全程檢測期末沖刺100分系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓C:![]() (
(![]() )的左右焦點分別為
)的左右焦點分別為![]()
![]() ,點
,點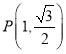 滿足:
滿足:![]() ,且
,且![]() .
.
(1)求橢圓C的標準方程;
(2)過點![]() 的直線l與C交于
的直線l與C交于![]() ,
,![]() 不同的兩點,且
不同的兩點,且![]() ,問在x軸上是否存在定點N,使得直線
,問在x軸上是否存在定點N,使得直線![]() ,
,![]() 與y軸圍成的三角形始終為底邊在y軸上的等腰三角形.若存在,求定點N的坐標;若不存在,請說明理由.
與y軸圍成的三角形始終為底邊在y軸上的等腰三角形.若存在,求定點N的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】袋子有5個不同的小球,編號分別為1,2,3,4,5,從袋中一次取出三個球,記隨機變量![]() 是取出球的最大編號與最小編號的差,數學期望為
是取出球的最大編號與最小編號的差,數學期望為![]() ,方差為
,方差為![]() 則下列選項正確的是( )
則下列選項正確的是( )
A.![]() ,
,![]() B.
B.![]() ,
,![]()
C.![]() ,
,![]() D.
D.![]() ,
,![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著生活節奏的加快以及智能手機的普及,外賣點餐逐漸成為越來越多用戶的餐飲消費習慣,由此催生了一批外賣點餐平臺.已知某外賣平臺的送餐費用與送餐距離有關(該平臺只給5千米范圍內配送),為調査送餐員的送餐收入,現從該平臺隨機抽取100名點外賣的用戶進行統計,按送餐距離分類統計結果如表:
送餐距離(千米) | (0,1] | (1,2] | (2,3] | (3,4] | (4,5] |
頻數 | 15 | 25 | 25 | 20 | 15 |
以這100名用戶送餐距離位于各區間的頻率代替送餐距離位于該區間的概率.
(1)若某送餐員一天送餐的總距離為100千米,試估計該送餐員一天的送餐份數;(四舍五入精確到整數,且同一組中的數據用該組區間的中點值為代表).
(2)若該外賣平臺給送餐員的送餐費用與送餐距離有關,規定2千米內為短距離,每份3元,2千米到4千米為中距離,每份7元,超過4千米為遠距離,每份12元.記X為送餐員送一份外賣的收入(單位:元),求X的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖①:在平行四邊形![]() 中,
中,![]() ,
,![]() ,將
,將![]() 沿對角線
沿對角線![]() 折起,使
折起,使![]() ,連結
,連結![]() ,得到如圖②所示三棱錐
,得到如圖②所示三棱錐![]() .
.
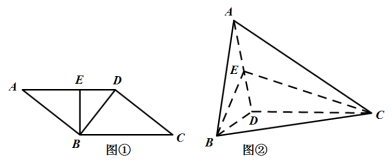
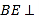
(1)證明:![]() 平面
平面![]() ;
;
(2)若![]() ,二面角
,二面角![]() 的平面角的正切值為
的平面角的正切值為![]() ,求直線
,求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某城市對一項惠民市政工程滿意程度(分值:![]() 分)進行網上調查,有2000位市民參加了投票,經統計,得到如下頻率分布直方圖(部分圖):
分)進行網上調查,有2000位市民參加了投票,經統計,得到如下頻率分布直方圖(部分圖):

現用分層抽樣的方法從所有參與網上投票的市民中隨機抽取![]() 位市民召開座談會,其中滿意程度在
位市民召開座談會,其中滿意程度在![]() 的有5人.
的有5人.
(1)求![]() 的值,并填寫下表(2000位參與投票分數和人數分布統計);
的值,并填寫下表(2000位參與投票分數和人數分布統計);
滿意程度(分數) |
|
|
|
|
|
人數 |
(2)求市民投票滿意程度的平均分(各分數段取中點值);
(3)若滿意程度在![]() 的5人中恰有2位為女性,座談會將從這5位市民中任選兩位發言,求男性甲或女性乙被選中的概率.
的5人中恰有2位為女性,座談會將從這5位市民中任選兩位發言,求男性甲或女性乙被選中的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】高鐵是我國國家名片之一,高鐵的修建凝聚著中國人的智慧與汗水.如圖所示,B、E、F為山腳兩側共線的三點,在山頂A處測得這三點的俯角分別為![]() 、
、![]() 、
、![]() ,計劃沿直線BF開通穿山隧道,現已測得BC、DE、EF三段線段的長度分別為3、1、2.
,計劃沿直線BF開通穿山隧道,現已測得BC、DE、EF三段線段的長度分別為3、1、2.

(1)求出線段AE的長度;
(2)求出隧道CD的長度.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com