f(x)為奇函數，當x＞0時，函數f(x)=sin 2x＋1，當x＜0時，f(x)的解析式是
[ ]
科目：高中數學 來源： 題型：
,k∈Z},且f(x+1)=-
,如果f(x)為奇函數，當0＜x＜
時，f(x)=3x. (1)求f(
)；
(2)當2k+
＜x＜2k+1(k∈Z)時，求f(x);
(3)是否存在這樣的正整數k，使得當2k+
＜x＜2k+1(k∈Z)時，log3f(x)＞x2-kx-2k有解？
查看答案和解析>>
科目：高中數學 來源： 題型：
已知f(x)為奇函數，當x>0，f(x)＝x(1＋x)，那么x<0，f(x)等于 ( )
A．－x(1－x) B．x(1－x)
C．－x(1＋x) D．x(1＋x)
查看答案和解析>>
科目：高中數學 來源：2013-2014學年人教版高考數學文科二輪專題復習提分訓練7練習卷（解析版） 題型：選擇題
已知函數f(x)為奇函數,且當x>0時,f(x)=x2+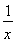
,則f(-1)等于( )
(A)2 (B)1 (C)0 (D)-2
查看答案和解析>>
科目：高中數學 來源： 題型：
.(1)求函數f(x)的表達式;
(2)設數列{an},{bn}滿足如下關系:an+1=
,bn=
(n∈N*),且b1=
,求數列{bn}的通項公式,并求數列{(3n-1)
bn}(n∈N*)前n項的和Sn.
(文)已知等差數列{an}滿足:an+1＞an(n∈N*),a1=1,該數列的前三項分別加上1,1,3后順次成為等比數列{bn}的前三項.
(1)分別求數列{an},{bn}的通項公式an,bn;
(2)設Tn=
(n∈N*),若Tn+
＜c(c∈Z)恒成立,求c的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
,則f(-1)= ( )