
分析 (1)求出函數的導數,根據導函數的符號,求出函數的單調區間即可;
(2)f(x)的最大值減去f(x)的最小值大于或等于e-1,由單調性知,f(x)的最大值是f(1)或f(-1),最小值f(0)=1,由f(1)-f(-1)的單調性,判斷f(1)與f(-1)的大小關系,再由f(x)的最大值減去最小值f(0)大于或等于e-1求出a的取值范圍.
解答 解:(1)∵f(x)=ax+x2-xlna,
∴f′(x)=axlna+2x-lna=(ax-1)lna+2x,
∵0<a<1或a>1,
∴當x∈(0,+∞)時,lna與ax-1同號,
∴f′(x)>0,∴函數在(0,+∞)上單調遞增.
x∈(-∞,0)時,lna與ax-1異號,
∴函數在(-∞,0)上單調遞減.
(2)∵存在x1,x2∈[-1,1],使得|f(x1)-f(x2)|≥e-1,
∴當x∈[-1,1]時,|(f(x))max-(f(x))min|=(f(x))max-(f(x))min≥e-1.
∵f(x)在[-1,0]上遞減,在[0,1]上遞增,
∴當x∈[-1,1]時,(f(x))min=f(0)=1,
(f(x))max=max{f(-1),f(1)},
而f(1)-f(-1)=(a+1-lna)-($\frac{1}{a}$+1+lna),
記g(t)=t-$\frac{1}{t}$-2lnt(t>0 ),
∵g′(t)=1+$\frac{1}{{t}^{2}}$-$\frac{2}{t}$=($\frac{1}{t}$-1)2≥0,(當t=1時取等號),
∴g(t)=t-$\frac{1}{t}$-2lnt(t>0 )在t∈(0,+∞)上單調遞增,而g(1)=0,
∴當t>1時,g(t)>0;當0<t<1時,g(t)<0.
也就是當a>1時,f(1)>f(-1);當0<a<1時,f(1)<f(-1);
①當a>1時,由f(1)-f(0)≥e-1⇒a-lna≥e-1⇒a≥e,
②當0<a<1時,由f(-1)-f(0)≥e-1,
可得$\frac{1}{a}$+lna≥e-1,$\frac{1}{e}$≥a>0
綜上知,所求a的取值范圍為 (0,$\frac{1}{e}$]∪[e,+∞).
點評 本題考查函數的零點,用導數判斷函數單調性,利用導數研究函數極值,屬于中檔題.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
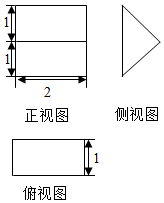 《九章算術》中,將底面是直角三角形的直三棱柱稱之為“塹堵”,已知某“塹堵”的三視圖如圖所示,則該“塹堵”的表面積為( )
《九章算術》中,將底面是直角三角形的直三棱柱稱之為“塹堵”,已知某“塹堵”的三視圖如圖所示,則該“塹堵”的表面積為( )| A. | 2 | B. | 4 | C. | 4+4$\sqrt{2}$ | D. | 6+4$\sqrt{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | x0<a | B. | x0>b | C. | x0<c | D. | x0>c |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com