【題目】在平面直角坐標系xOy中，直線l的參數方程為
（t為參數），曲線C的參數方程為
（θ為參數）.
（1）當
時，求直線l與曲線C的普通方程；
（2）若直線l與曲線C交于A，B兩點，直線l傾斜角的范圍為（0，
]，且P點的直角坐標為（0，2），求
的最小值.
【答案】（1）
；（x+1）2+（y﹣1）2＝1（2）
【解析】
（1）將
代入直線l的參數方程，消去參數t即可得到直線l的普通方程，由曲線C的參數方程消去參數θ即可得到曲線C的普通方程；
（2）利用參數的幾何意義結合正弦型函數的圖象及性質即可得解.
（1）∵，
∴直線l的參數方程為
，消掉參數t，可得直線l的普通方程為
，
∵C的參數方程為
（θ為參數）
∴可得（x+1）2+（y﹣1）2＝1，即曲線C的普通方程為（x+1）2+（y﹣1）2＝1.
（2）將l的參數方程為
（t為參數）代入圓的方程（x+1）2+（y﹣1）2＝1得t2+2（sinα+cosα）t+1＝0，
設A，B所對應的參數分別為t1，t2，
則|PA||PB|＝|t1t2|＝1，|PA|+|PB|＝|t1+t2|＝2|sinα+cosα|，
所以
，
當
時，
的最小值為
.
科目：高中數學 來源： 題型：
【題目】在直角坐標系
中，曲線
，曲線
（
為參數），以坐標原點
為極點，以
軸的正半軸為極軸建立極坐標系.
（1）求
的極坐標方程；
（2）射線
的極坐標方程為
，若分別與交于異于極點的
兩點，求
的最大值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知雙曲線
的虛軸的一個頂點為
，左頂點為
，雙曲線
的左、右焦點分別為
，
，點
為線段
上的動點，當
取得最小值和最大值時，
的面積分別為
，
，若
，則雙曲線的離心率為（ ）．
A.
B.
C.
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下圖是2020年2月15日至3月2日武漢市新增新冠肺炎確診病例的折線統計圖．則下列說法不正確的是（ ）
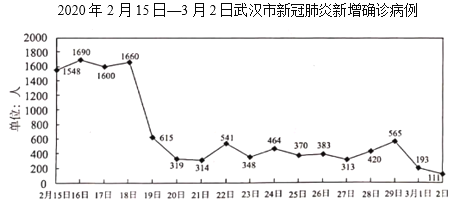
A.2020年2月19日武漢市新增新冠肺炎確診病例大幅下降至三位數
B.武漢市在新冠肺炎疫情防控中取得了階段性的成果，但防控要求不能降低
C.2020年2月19日至3月2日武漢市新增新冠肺炎確診病例低于400人的有8天
D.2020年2月15日到3月2日武漢市新增新冠肺炎確診病例最多的一天比最少的一天多1549人
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知
，有下列4個命題：
①若
，則
的圖象關于直線
對稱；
②
與
的圖象關于直線
對稱；
③若為偶函數，且
，則的圖象關于直線對稱；
④若為奇函數，且
，則的圖象關于直線對稱.
其中正確的命題為 .（填序號）
查看答案和解析>>
科目：高中數學 來源： 題型：
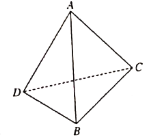
【題目】現有一副斜邊長為10的直角三角板，將它們斜邊
重合，若將其中一個三角板沿斜邊折起形成三棱錐
，如圖所示，已知
，
，則三棱錐的外接球的表面積為______；該三棱錐體積的最大值為_______．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知動直線與
與橢圓
交于
、
兩不同點，且
的面積
，其中
為坐標原點
（1）若動直線垂直于
軸.求直線的方程；
（2）證明：
和
均為定值；
（3）橢圓
上是否存在點
，
，
，使得三角形面積
若存在，判斷
的形狀；若不存在，請說明理由
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知拋物線
：
的焦點為
，過焦點做傾斜角為的120°的直線交于
，
兩點，
為坐標原點，
．
（1）求拋物線的方程；
（2）過拋物線焦點，且與坐標軸不垂直的直線l交拋物線于
，
兩點，
，
在拋物線上，且
，
，若，，，四點都在圓
上，求圓的方程．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】定義：
是無窮數列，若存在正整數k使得對任意
，均有
則稱是近似遞增（減）數列，其中k叫近似遞增（減）數列的間隔數
（1）若
，是不是近似遞增數列，并說明理由
（2）已知數列的通項公式為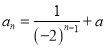
，其前n項的和為
，若2是近似遞增數列
的間隔數，求a的取值范圍：
（3）已知
，證明是近似遞減數列，并且4是它的最小間隔數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com