
分析 (Ⅰ)運用橢圓的離心率公式和點滿足方程及a,b,c的關系,即可得到橢圓方程;
(Ⅱ)設直線l的方程設為y=kx+t,設A(x1,y1)B(x2,y2),聯立橢圓方程,運用韋達定理和判別式大于0,以AB為直徑的圓過坐標原點,則有$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,x1x2+y1y2=0,代入化簡整理,再由兩直線垂直的條件,解方程可得k,進而得到所求直線方程.
解答 解:(Ⅰ)由橢圓的離心率e=$\frac{c}{a}$=$\sqrt{1-\frac{{b}^{2}}{{a}^{2}}}$=$\frac{\sqrt{3}}{2}$,則a2=4b2,
由|PA|=a-$\frac{3}{4}$,|PB|=$\sqrt{{b}^{2}+(\frac{3}{4})^{2}}$,
|PA|=|PB|.即a-$\frac{3}{4}$=$\sqrt{{b}^{2}+(\frac{3}{4})^{2}}$,
解得:a=2,b=1,
∴橢圓的標準方程為:$\frac{{x}^{2}}{4}+{y}^{2}=1$;
(Ⅱ)設直線l的方程設為y=kx+t,設M(x1,y1)N(x2,y2),
聯立$\left\{\begin{array}{l}{y=kx+t}\\{{x}^{2}+4{y}^{2}=4}\end{array}\right.$,消去y得(1+4k2)x2+8ktx+4t2-4=0,
則有x1+x2=$\frac{-8kt}{1+4{k}^{2}}$,x1x2=$\frac{4{t}^{2}-4}{1+4{k}^{2}}$,
由△>0,可得4k2+1>t2,
y1+y2=kx1+t+kx2+t=k(x1+x2)+2t=$\frac{2t}{1+4{k}^{2}}$,
y1y2=(kx1+t)(kx2+t)=k2x1x2+kt(x1+x2)+t2=k2•$\frac{4{t}^{2}-4}{1+4{k}^{2}}$+kt•$\frac{-8kt}{1+4{k}^{2}}$+t2=$\frac{{t}^{2}-4{k}^{2}}{1+4{k}^{2}}$,
因為以AB為直徑的圓過坐標原點,
所以$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,即為x1x2+y1y2=0,
即為$\frac{4{t}^{2}-4}{1+4{k}^{2}}$+$\frac{{t}^{2}-4{k}^{2}}{1+4{k}^{2}}$=0,可得5t2=4+4k2,①
由4k2+1>t2,可得t>$\frac{\sqrt{3}}{2}$或t<-$\frac{\sqrt{3}}{2}$,
又設AB的中點為D(m,n),則m=$\frac{{x}_{1}+{x}_{2}}{2}$=$\frac{-4kt}{1+4{k}^{2}}$,n=$\frac{{y}_{1}+{y}_{2}}{2}$=$\frac{t}{1+4{k}^{2}}$,
因為直線PD與直線l垂直,所以kPD=-$\frac{1}{k}$=$\frac{0-n}{\frac{3}{4}-m}$=$\frac{-\frac{t}{1+4{k}^{2}}}{\frac{3}{4}+\frac{4kt}{1+4{k}^{2}}}$,可整理得:t=-$\frac{1+4{k}^{2}}{4k}$②
解得:k2=$\frac{1}{4}$,k2=$\frac{5}{4}$,
當k=$\frac{1}{2}$時,t=-1,當k=-$\frac{1}{2}$,t=1,
當k=$\frac{\sqrt{5}}{2}$,t=-$\frac{3\sqrt{5}}{5}$,
當k=-$\frac{\sqrt{5}}{2}$,t=$\frac{3\sqrt{5}}{5}$,
滿足△>0,
所以直線l的方程為y=$\frac{1}{2}$x-1,y=-$\frac{1}{2}$x+1,y=$\frac{\sqrt{5}}{2}$x-$\frac{3\sqrt{5}}{5}$,y=-$\frac{\sqrt{5}}{2}$x+$\frac{3\sqrt{5}}{5}$.
點評 本題考查橢圓的方程和性質,主要考查橢圓的離心率的運用和方程的運用,聯立直線方程,運用韋達定理,同時考查圓的性質:直徑所對的圓周角為直角,考查直線垂直的條件和直線方程的求法,屬于中檔題.


 勵耘書業暑假銜接寧波出版社系列答案
勵耘書業暑假銜接寧波出版社系列答案科目:高中數學 來源: 題型:選擇題
| A. | $\frac{17}{3}$ | B. | $\frac{22}{3}$ | C. | $\frac{32}{3}$ | D. | $\frac{35}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
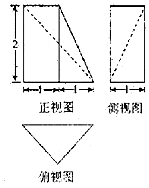
| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | 2 | D. | $\frac{8}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{16}{3}$π | B. | 16π | C. | $\frac{64}{3}$π | D. | 64π |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題

查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
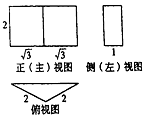
| A. | $4+4\sqrt{3}$ | B. | $4+6\sqrt{3}$ | C. | $8+6\sqrt{3}$ | D. | $8+8\sqrt{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com