【題目】已知向量 
=（sinA，cosA）， 
=（cosB，sinB）， 
=sin2C且A、B、C分別為△ABC的三邊a，b，c所對的角．
（1）求角C的大小；
（2）若sinA，sinC，sinB成等比數列，且 
=18，求c的值．．
【答案】
（1）解：∵ 
=sin2C
∴sinAcosB+sinBcosA=sin2C
∴sin（A+B）=sinC=sin2C=2sinCcosC
∵sinC≠0
∴cosC= 
∵C∈（0，π）
∴ 
（2）解：∵sinA，sinB，sinB成等比數列，
∴sin2C=sinAsinB
由正弦定理可得c2=ab
∵ 
=18，
∴ 
= 
=18，
∴ab=36
∴c2=36，c=6
【解析】（1）由 =sin2C，結合向量的數量積的坐標表示及兩角和的正弦公式可求cosC，進而可求C（2）由已知可得，sin2C=sinAsinB，結合正弦定理可得c2=ab，再由向量的數量積的定義可求ab，進而可求c
【考點精析】利用等比數列的通項公式（及其變式）和正弦定理的定義對題目進行判斷即可得到答案，需要熟知通項公式：
；正弦定理:
．
桃李文化快樂暑假武漢出版社系列答案
優秀生快樂假期每一天全新寒假作業本系列答案
暑假接力賽新疆青少年出版社系列答案科目：高中數學 來源： 題型：
【題目】定義：如果函數y=f（x）在定義域內給定區間[a，b]上存在x0（a＜x0＜b），滿足f（x0）= 
，則稱函數y=f（x）是[a，b]上的“平均值函數”，x0是它的一個均值點．例如y=|x|是[﹣2，2]上的平均值函數，0就是它的均值點．若函數f（x）=x2﹣mx﹣1是[﹣1，1]上的“平均值函數”，則實數m的取值范圍是 ．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設數列{an}的前n項和為Sn ， 對任意的正整數n，都有an=5Sn+1成立，記bn= 
（n∈N*）．
（1）求數列{an}和數列{bn}的通項公式；
（2）設數列{bn}的前n項和為Rn ， 求證：對任意的n∈N* ， 都有Rn＜4n；
（3）記cn=b2n﹣b2n﹣1（n∈N*），設數列{cn}的前n項和為Tn ， 求證：對任意n∈N* ， 都有Tn＜ 
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知正方形ABCD的頂點坐標分別為A（0，1），B（2，0），C（3，2）．
（1）求CD邊所在直線的方程；
（2）求以AC為直徑的圓M的標準方程．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，菱形ABCD的邊長為2，△BCD為正三角形，現將△BCD沿BD向上折起，折起后的點C記為C′，且CC′= 
，連接CC′，E為CC′的中點．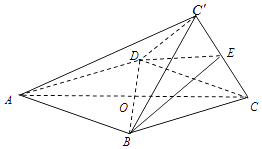 
文科：
（1）求證：AC′∥平面BDE；
（2）求證：CC′⊥平面BDE；
（3）求三棱錐C′﹣BCD的體積．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知A、B、C為△ABC的三個內角，且其對邊分別為a、b、c，若cosBcosC﹣sinBsinC= 
．
（1）求角A；
（2）若a=2 
，b+c=4，求△ABC的面積．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列四個命題中，正確的有（ ） ①兩個變量間的相關系數r越小，說明兩變量間的線性相關程度越低；
②命題“x∈R，使得x2+x+1＜0”的否定是：“對x∈R，均有x2+x+1＞0”；
③命題“p∧q為真”是命題“p∨q為真”的必要不充分條件；
④若函數f（x）=x3+3ax2+bx+a2在x=﹣1有極值0，則a=2，b=9或a=1，b=3．
A.0 個
B.1 個
C.2 個
D.3個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com